1.(2024·苏州中考)下列图案中,是轴对称图形的是( ).

A.
B.
C.
D.

A.
B.
C.
D.
答案:
A
2.(2025·江苏无锡锡山区期末)已知点$A(-3,2)和点B(m,n)$关于x轴对称,则n的值为( ).
A.-3
B.3
C.-2
D.2
A.-3
B.3
C.-2
D.2
答案:
C [解析]
∵点A(−3,2)和点B(m,n)关于x轴对称,
∴m=−3,n=−2.故选C.
知识拓展 对于点(a,b)来说,有关对称的关系:
关于原点对称 (−a,−b)
关于x轴对称的坐标 (a,−b)
对称 关于y轴对称的坐标 (−a,b)
性 关于x=a对称 (2a−x,y)
关于y=b对称 (x,2b−y)
关于y=x对称 (y,x)
∵点A(−3,2)和点B(m,n)关于x轴对称,
∴m=−3,n=−2.故选C.
知识拓展 对于点(a,b)来说,有关对称的关系:
关于原点对称 (−a,−b)
关于x轴对称的坐标 (a,−b)
对称 关于y轴对称的坐标 (−a,b)
性 关于x=a对称 (2a−x,y)
关于y=b对称 (x,2b−y)
关于y=x对称 (y,x)
3.(2025·云南昆明期末)大观公园是国家4A级旅游景区,始建于明朝洪武元年(公元1368年),位于昆明市以西约2公里的滇池湖畔,完好保存着许多古典园林建筑群,既反映中国清代古建筑的风格,又具有云南地方民族建筑的特色,是云南清代园林建筑的博览苑.如图,建筑的顶端可看作等腰三角形ABC,$AB= AC$,D是BC的中点.下列结论不一定正确的是( ).
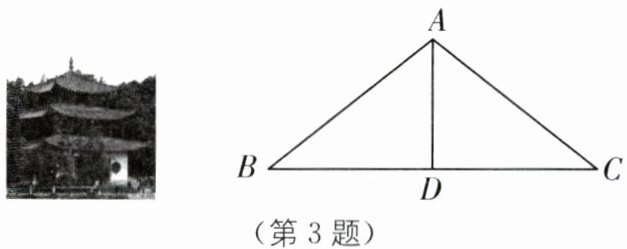
A.$∠B= ∠C$
B.$AD⊥BC$
C.$∠BAD= ∠CAD$
D.$AB= 2AD$

A.$∠B= ∠C$
B.$AD⊥BC$
C.$∠BAD= ∠CAD$
D.$AB= 2AD$
答案:
D
4.(2025·安徽合肥科大附中期末)如图,$AB= AC= AD,∠BAD= 50^{\circ }$,则$∠BCD$的度数为( ).
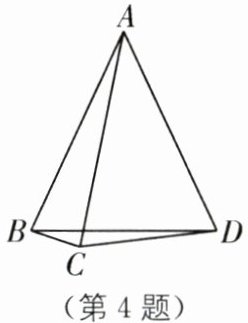
A.$115^{\circ }$
B.$130^{\circ }$
C.$140^{\circ }$
D.$155^{\circ }$

A.$115^{\circ }$
B.$130^{\circ }$
C.$140^{\circ }$
D.$155^{\circ }$
答案:
D [解析]
∵∠BAD=50°,
∴∠ABC+∠BCD+∠ADC=180°×2−50°=310°,
∴∠ABC+∠ACB+∠ACD+∠ADC=310°.
∵AB=AC=AD,
∴∠ABC=∠ACB,∠ACD=∠ADC,
∴∠BCD=∠ACB+∠ACD=$\frac{1}{2}$×310°=155°.故选D.
∵∠BAD=50°,
∴∠ABC+∠BCD+∠ADC=180°×2−50°=310°,
∴∠ABC+∠ACB+∠ACD+∠ADC=310°.
∵AB=AC=AD,
∴∠ABC=∠ACB,∠ACD=∠ADC,
∴∠BCD=∠ACB+∠ACD=$\frac{1}{2}$×310°=155°.故选D.
5.(2025·浙江金华永康期末)如图,在$△ABC$中,D,E为BC边上两点,且满足$AB= BE,AC= CD$,连接AD,AE.若$∠BAC= 100^{\circ }$,则$∠DAE$的度数为( ).
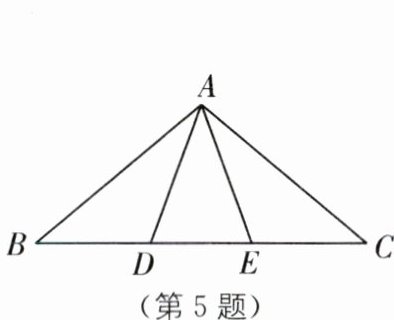
A.$45^{\circ }$
B.$40^{\circ }$
C.$35^{\circ }$
D.$30^{\circ }$

A.$45^{\circ }$
B.$40^{\circ }$
C.$35^{\circ }$
D.$30^{\circ }$
答案:
B [解析]
∵∠BAC=100°,
∴∠B+∠C=180°−100°=80°.
∵AB=BE,
∴∠BEA=∠BAE,
∴∠BEA=$\frac{1}{2}$×(180°−∠B)=90°−$\frac{1}{2}$∠B,
同理可得∠ADC=90°−$\frac{1}{2}$∠C,
∴∠BEA+∠ADC=180°−$\frac{1}{2}$(∠B+∠C),
∴∠DAE=180°−(∠BEA+∠ADC)=$\frac{1}{2}$(∠B+∠C)=
40°.故选B.
∵∠BAC=100°,
∴∠B+∠C=180°−100°=80°.
∵AB=BE,
∴∠BEA=∠BAE,
∴∠BEA=$\frac{1}{2}$×(180°−∠B)=90°−$\frac{1}{2}$∠B,
同理可得∠ADC=90°−$\frac{1}{2}$∠C,
∴∠BEA+∠ADC=180°−$\frac{1}{2}$(∠B+∠C),
∴∠DAE=180°−(∠BEA+∠ADC)=$\frac{1}{2}$(∠B+∠C)=
40°.故选B.
6.(2025·江苏镇江句容期末)若点$M(-2,1)与点N(-2,3)$关于某条直线对称,则这条直线是( ).
A.x轴
B.y轴
C.过点$(-2,0)$且垂直于x轴的直线
D.过点$(0,2)$且平行于x轴的直线
A.x轴
B.y轴
C.过点$(-2,0)$且垂直于x轴的直线
D.过点$(0,2)$且平行于x轴的直线
答案:
D[解析]
∵点M(−2,1)与点N(−2,3),
∴MN//y轴,设MN的中点为A,
则A点坐标为(−2,$\frac{1+3}{2}$),即A(−2,2),
∴点M(−2,1)与点N(−2,3)关于某条直线对称,这条直线是过点(0,2)且平行于x轴的直线.故选D.
∵点M(−2,1)与点N(−2,3),
∴MN//y轴,设MN的中点为A,
则A点坐标为(−2,$\frac{1+3}{2}$),即A(−2,2),
∴点M(−2,1)与点N(−2,3)关于某条直线对称,这条直线是过点(0,2)且平行于x轴的直线.故选D.
7.分类讨论思想(2024·广西梧州岑溪期末)已知一个等腰三角形有两内角的度数之比为$1:4$,则这个等腰三角形顶角的度数为( ).
A.$20^{\circ }$
B.$120^{\circ }$
C.$20^{\circ }或120^{\circ }$
D.$36^{\circ }$
A.$20^{\circ }$
B.$120^{\circ }$
C.$20^{\circ }或120^{\circ }$
D.$36^{\circ }$
答案:
C [解析]设两内角的度数为x,4x.
当等腰三角形的顶角为x时,x+4x+4x=180°,解得x=
20°;当等腰三角形的顶角为4x时,4x+x+x=180°,解得x=30°,
∴4x=120°.因此等腰三角形的顶角度数为20°或120°.故选C;
思路引导 掌握20°或120°都有做顶角的可能是解题的突破口,
当等腰三角形的顶角为x时,x+4x+4x=180°,解得x=
20°;当等腰三角形的顶角为4x时,4x+x+x=180°,解得x=30°,
∴4x=120°.因此等腰三角形的顶角度数为20°或120°.故选C;
思路引导 掌握20°或120°都有做顶角的可能是解题的突破口,
8.(2024·湖北襄阳期末)如图,在$△ABC$中,$AC= BC,AB= 6,△ABC$的面积为 12,$CD⊥AB$于点D,直线EF垂直平分BC交AB于点E,交BC于点F,P是线段EF上的一个动点,则$△PBD$的周长的最小值是( ).
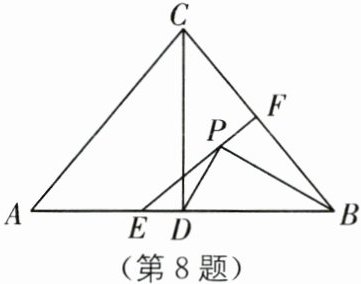
A.6
B.7
C.10
D.12

A.6
B.7
C.10
D.12
答案:
B [解析]如图,连接CP.
∵AC=BC,CD⊥AB,
∴BD=AD=3.
∵S△ABC=$\frac{1}{2}$AB·CD=
 12,
12,
∴CD=4.
∵EF垂直平分BC,
∴PB=PC,
∴PB+PD=PC+PD.
∵PC+PD≥CD,
∴PC+PD≥4,
∴PC+PD的最小值为4,
∴△PBD的周长的最小值为4+3=7.故选B、
B [解析]如图,连接CP.
∵AC=BC,CD⊥AB,
∴BD=AD=3.
∵S△ABC=$\frac{1}{2}$AB·CD=
 12,
12,∴CD=4.
∵EF垂直平分BC,
∴PB=PC,
∴PB+PD=PC+PD.
∵PC+PD≥CD,
∴PC+PD≥4,
∴PC+PD的最小值为4,
∴△PBD的周长的最小值为4+3=7.故选B、
查看更多完整答案,请扫码查看


