《2025年实验班提优训练八年级数学上册人教版》

24.(2025·内蒙古通辽期末)阅读材料:利用公式法,可以将一些形如$ax^{2} + bx + c(a ≠ 0)的多项式变形为a(x + m)^{2} + n$的形式,我们把这样的变形方法叫作多项式$ax^{2} + bx + c(a ≠ 0)$的配方法,运用多项式的配方法及平方差公式能对一些多项式进行因式分解.
例如:$x^{2} + 4x - 5 = x^{2} + 4x + (\frac{4}{2})^{2} - (\frac{4}{2})^{2} - 5 = (x + 2)^{2} - 9 = (x + 2 + 3)(x + 2 - 3) = (x + 5)(x - 1)$;
$x^{2} + 6x - 7 = x^{2} + 6x + (\frac{6}{2})^{2} - (\frac{6}{2})^{2} - 7 = (x + 3)^{2} - 16 = (x + 3 + 4)(x + 3 - 4) = (x + 7)(x - 1)$.
根据以上材料,解答下列问题:
(1)分解因式:$x^{2} + 2x - 8$;
(2)求多项式$x^{2} + 4x - 3$的最小值;
(3)已知$a,b,c是\triangle ABC$的三边长,且满足$a^{2} + b^{2} + c^{2} + 50 = 6a + 8b + 10c$,求$\triangle ABC$的周长.

答案：
(1)$x^{2}+2x-8=x^{2}+2x+1-1-8=(x+1)^{2}-9=(x+1-3)(x+1+3)=(x-2)(x+4)$.
(2)$x^{2}+4x-3=x^{2}+4x+(\frac{4}{2})^{2}-(\frac{4}{2})^{2}-3=(x+2)^{2}-7$.
∵$(x+2)^{2}\geq0$，
∴$(x+2)^{2}-7\geq-7$，
∴多项式$x^{2}+4x-3$的最小值为$-7$.
(3)
∵$a^{2}+b^{2}+c^{2}+50=6a+8b+10c$，
∴$a^{2}+b^{2}+c^{2}+50-6a-8b-10c=0$，
∴$a^{2}-6a+9+b^{2}-8b+16+c^{2}-10c+25-9-16-25+50=0$，
∴$(a-3)^{2}+(b-4)^{2}+(c-5)^{2}=0$，
∴$a-3=0$，$b-4=0$，$c-5=0$，
∴$a=3$，$b=4$，$c=5$，
∴△ABC的周长$=3+4+5=12$.

25.中考新考法 解题策略开放 如图(1),有$A,B,C$三种不同型号的卡片若干张,其中$A型是边长为a(a ＞ b)$的正方形,$B型是长为a$、宽为$b$的长方形,$C型是边长为b$的正方形.
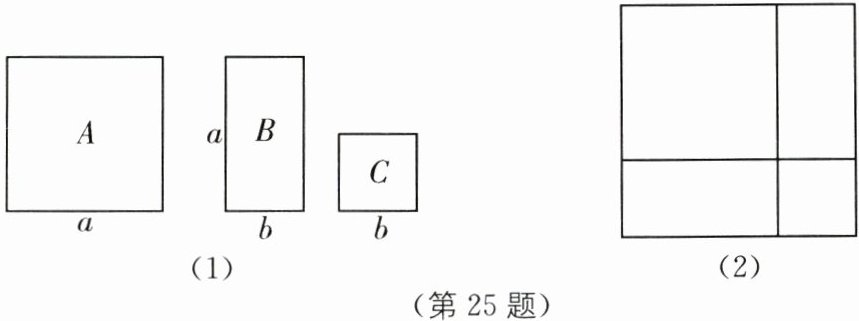
(1)若用$A$型卡片1张,$B$型卡片2张,$C$型卡片1张拼成了一个正方形(如图(2)),此正方形的边长为____,根据该图形请写出一条属于因式分解的等式:____.
(2)若要拼一个长为$2a + b$,宽为$a + 2b$的长方形,设需要$A类卡片x$张,$B类卡片y$张,$C类卡片z$张,则$x + y + z = $____.
(3)现有$A$型卡片1张,$B$型卡片6张,$C$型卡片11张,从这18张卡片中拿掉两张卡片,余下的卡片全用上,你能拼出一个长方形或正方形吗? 有几种拼法? 请你通过运算说明理由.

答案：
(1)$a+b$ $a^{2}+2ab+b^{2}=(a+b)^{2}$
(2)9
(3)四种拼法：第一种：A型卡片拿掉1张，B型卡片拿掉1张，则能拼出一个长方形，即长方形的长为$5a+11b$，宽为b，
∴$b(5a+11b)=5ab+11b^{2}$；第二种：A型卡片拿掉1张，C型卡片拿掉1张，则能拼出一个长方形，即长方形的长为$3a+5b$，宽为2b或者长为$6a+10b$，宽为b，
∴$2b(3a+5b)=6ab+10b^{2}$或$(6a+10b)b=6ab+10b^{2}$，此种情况共2种拼法；第三种：C型卡片拿掉2张，则能拼出一个正方形，即正方形边长为$a+3b$，
∴$(a+3b)^{2}=a^{2}+6ab+9b^{2}$. 故共有4种拼法.