《2025年实验班提优训练八年级数学上册人教版》

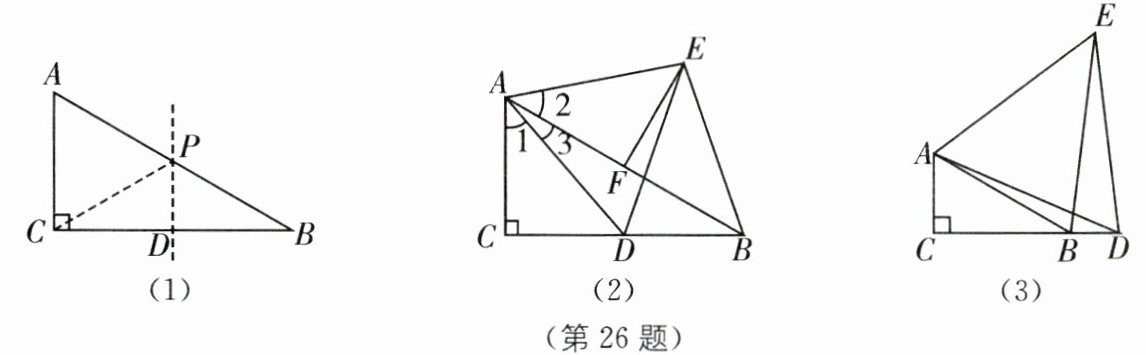
26.问题探究:如图(1),在$Rt△ABC$中,$∠ACB= 90^{\circ },∠ABC= 30^{\circ }$,为探究$Rt△ABC中30^{\circ }$角所对的直角边AC与斜边AB的数量关系,学习小组成员已经添加了辅助线.
(1)请叙述辅助线的添法,并完成探究过程;
探究应用1:如图(2),在$Rt△ABC$中,$∠C= 90^{\circ },∠ABC= 30^{\circ }$,点D在线段CB上,以AD为边作等边三角形ADE,连接BE,为探究线段BE与DE之间的数量关系,组长已经添加了辅助线:取AB的中点F,连接EF.
(2)线段BE与DE之间的数量关系为____,并说明理由;
探究应用2:如图(3),在$Rt△ABC$中,$∠C= 90^{\circ },∠ABC= 30^{\circ }$,点D在线段CB的延长线上,以AD为边作等边三角形ADE,连接BE.
(3)线段BE与DE之间的数量关系为____,并说明理由.

答案：
(1)作CB的垂直平分线分别交AB,BC于点P,D,连接PC,
∴PC=PB,
∴∠PCB=∠B=30°.
∵∠ACB=90°,
∴∠A=60°,∠ACP=60°,
∴∠APC=∠A=∠ACP=60°,
∴△ACP是等边三角形,
∴AC=AP=PC,
∴AC=AP=PB=$\frac{1}{2}$AB,即AC=$\frac{1}{2}$AB.
(2)BE=DE.理由如下:
∵F是AB的中点，
∴AF=$\frac{1}{2}$AB.
∵∠C=90°,∠ABC=30°,
∴AC=$\frac{1}{2}$AB,∠CAB=60°,
∴AC=AF.
∵△ADE是等边三角形，
∴AD=AE=DE,∠EAD=60°,
∴∠CAB=∠DAE,
∴∠CAB−∠3=∠DAE−∠3,即∠1=∠2.
　　　　　　　　　　　　　　AC=AF,
　　在△ACD和△AFE中,∠1=∠2,
　　　　　　　　　　　　　　AD=AE,
∴△ACD≌△AFE(SAS),
∴∠C=∠AFE=90°,
∴EF⊥AB.
∵F是AB的中点,
∴EF是AB的垂直平分线，
∴AE=BE,
∴BE=DE.
(3)BE=DE.理由如下:
取AB的中点F,连接EF,
∴AF=$\frac{1}{2}$AB.
∵∠C=90°,∠ABC=30°,
∴AC=$\frac{1}{2}$AB,∠CAB=60°.
∴AC=AF.
∵△ADE是等边三角形，
∴AD=AE=DE,∠EAD=60°.
∴∠CAB=∠DAE,
∴∠CAB+∠BAD=∠DAE+∠BAD,即∠CAD=∠BAE.
AC=AF,
在△ACD和△AFE中，∠CAD=∠FAE,
AD=AE,
　　　　　　　　　　{
∴△ACD≌△AFE(SAS),
∴∠C=∠AFE=90°,
∴EF⊥AB.
∵F是AB的中点,
∴EF是AB的垂直平分线，
∴AE=BE,
∴BE=DE.