《2025年实验班提优训练八年级数学上册人教版》

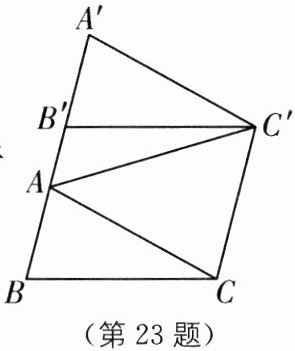
23.如图,将三角形ABC沿射线BA方向平移到三角形A'B'C'的位置,连接AC'.
(1)AA'与CC'的位置关系为______;
(2)求证:∠A'+∠CAC'+∠AC'C= 180°;
(3)设∠AC'B'= x,∠ACB= y,试探索∠CAC'与x,y之间的数量关系,并证明你的结论.

答案：

(1)AA'//CC'
(2)根据平移的性质可知A'C'//AC，AA'//CC'，
∴∠A'=∠BAC，∠BAC=∠ACC'，
∴∠A'=∠ACC'.
∵∠ACC'+∠CAC'+∠AC'C=180°，
∴∠A'+∠CAC'+∠AC'C=180°.
(3)∠CAC'=x+y.证明如下：如图，过点A作AD//BC，交CC'于点D.

根据平移的性质可知B'C'//BC，
∴B'C'//AD//BC，
∴∠AC'B'=∠C'AD，∠ACB=∠DAC.
∴∠CAC'=∠C'AD+∠CAD=∠AC'B'+∠ACB=x+y，即∠CAC'=x+y.

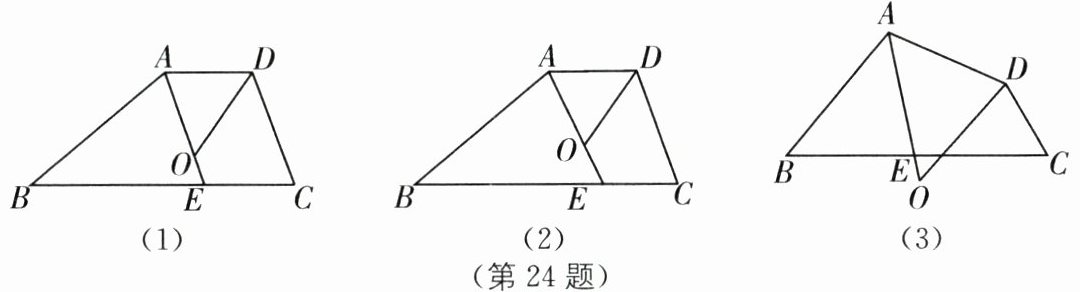
24.在四边形ABCD中,∠BAD的平分线与边BC交于点E,∠ADC的平分线交直线AE于点O.
(1)若点O在四边形ABCD的内部,
①如图(1),若AD//BC,∠B= 40°,∠C= 70°,则∠DOE= ______°;
②如图(2),试探索∠B,∠C,∠DOE之间的数量关系,并将你的探索过程写下来.
(2)如图(3),若点O在四边形ABCD的外部,请你直接写出∠B,∠C,∠DOE之间的数量关系.

答案：
(1)①125②∠B+∠C+2∠DOE=360°.理由如下：
∵AE，DO分别平分∠BAD，∠ADC，
∴∠OAD=$\frac{1}{2}$∠BAD，∠ADO=$\frac{1}{2}$∠ADC.
∵∠DOE=∠OAD+∠ADO，
∴2∠DOE=∠BAD+∠ADC.
∵∠B+∠C+∠BAD+∠ADC=360°，
∴∠B+∠C+2∠DOE=360°.
(2)∠B+∠C=2∠DOE.理由如下：
∵AE，DO分别平分∠BAD，∠ADC，
∴∠BAD=2∠EAD，∠ADC=2∠ADO.
∴∠BAD+∠ADC=2(∠EAD+∠ADO).
∵∠BAD+∠ADC=360°-∠B-∠C，∠EAD+∠ADO=180°-∠DOE，
∴360°-∠B-∠C=2(180°-∠DOE).
∴∠B+∠C=2∠DOE.