10.定义:如果$a^{x}= N(a>0,a≠1)$,那么x叫作以a为底N的对数,记做$x= log_{a}N$.例如:因为$7^{2}= 49$,所以$log_{7}49= 2$;因为$5^{3}= 125$,所以$log_{5}125= 3$,则下列说法正确的个数为( ).
①$log_{6}1= 0$;②$log_{3}2^{3}= 3log_{3}2$;③若$log_{2}(3-a)= log_{8}27$,则$a= 0$;④$log_{2}(xy)= log_{2}x+log_{2}y(x>0,y>0).$
A.4
B.3
C.2
D.1
①$log_{6}1= 0$;②$log_{3}2^{3}= 3log_{3}2$;③若$log_{2}(3-a)= log_{8}27$,则$a= 0$;④$log_{2}(xy)= log_{2}x+log_{2}y(x>0,y>0).$
A.4
B.3
C.2
D.1
答案:
A [解析]
∵6⁰=1,
∴log₆1=0,说法①符合题意;由于dᵐ·dⁿ=dᵐ⁺ⁿ,设M=dᵐ,N=dⁿ,则m=log_dM,n=log_dN,于是log_d(MN)=log_d(dᵐ·dⁿ)=log_d(dᵐ⁺ⁿ)=m+n=log_dM+log_dN,说法④符合题意;则log₃2³=log₃(2×2×2)=log₃2+log₃2+log₃2=3log₃2,说法②符合题意;设p=log_a b,则aᵖ=b,两边同时取以c为底的对数,log_c aᵖ=log_c b,则log_c aᵖ=plog_c a,plog_c a=log_c b,所以p=(log_c b)/(log_c a),即log_a b=(log_c b)/(log_c a).则log₈27=(log₂27)/(log₂8)=(1/3)log₂27=(1/3)log₂3³=3×(1/3)log₂3=log₂3.
∵log₂(3-a)=log₈27=log₂3,
∴a=0,说法③符合题意.故选A.
∵6⁰=1,
∴log₆1=0,说法①符合题意;由于dᵐ·dⁿ=dᵐ⁺ⁿ,设M=dᵐ,N=dⁿ,则m=log_dM,n=log_dN,于是log_d(MN)=log_d(dᵐ·dⁿ)=log_d(dᵐ⁺ⁿ)=m+n=log_dM+log_dN,说法④符合题意;则log₃2³=log₃(2×2×2)=log₃2+log₃2+log₃2=3log₃2,说法②符合题意;设p=log_a b,则aᵖ=b,两边同时取以c为底的对数,log_c aᵖ=log_c b,则log_c aᵖ=plog_c a,plog_c a=log_c b,所以p=(log_c b)/(log_c a),即log_a b=(log_c b)/(log_c a).则log₈27=(log₂27)/(log₂8)=(1/3)log₂27=(1/3)log₂3³=3×(1/3)log₂3=log₂3.
∵log₂(3-a)=log₈27=log₂3,
∴a=0,说法③符合题意.故选A.
11.(2024·河南驻马店期末)若$a^{2}+a-5= 0$,则代数式$(a^{2}-5)(a+1)$的值为____.
答案:
-5 [解析]
∵a²+a-5=0,
∴a²-5=-a,a²+a=5,
∴(a²-5)(a+1)=-a(a+1)=-(a²+a)=-5.
∵a²+a-5=0,
∴a²-5=-a,a²+a=5,
∴(a²-5)(a+1)=-a(a+1)=-(a²+a)=-5.
12.(2025·北京燕山地区期末)图中的四边形均为长方形,请你根据图形面积写出一个正确的等式:____.
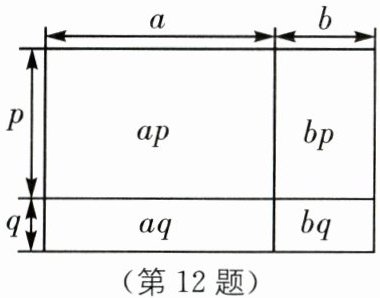

答案:
(a+b)(p+q)=ap+aq+bp+bq(答案不唯一)
13.(2025·重庆期末)如果整式$(ax^{2}-x+1)(bx-2)的计算结果中不含x^{2}$项和x项,那么$ab= $____.
答案:
-2 [解析]
∵多项式(ax²-x+1)(bx-2)=abx³+(-2a-b)x²+(b+2)x-2不含x²项和x项,
∴-2a-b=0且b+2=0,解得a=1,b=-2,
∴ab=-2.
∵多项式(ax²-x+1)(bx-2)=abx³+(-2a-b)x²+(b+2)x-2不含x²项和x项,
∴-2a-b=0且b+2=0,解得a=1,b=-2,
∴ab=-2.
14.如图,两个正方形的边长分别为m,n,如果$m+n= mn= 5$,则阴影部分的面积为____.
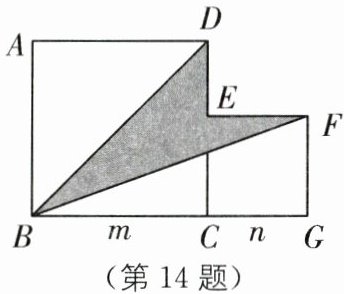

答案:
5 [解析]
∵两个正方形边长分别为m,n,
∴阴影部分的面积为m²+n²-(1/2)m²-(1/2)(m+n)n=m²+n²-(1/2)m²-(1/2)mn-(1/2)n²=(1/2)m²-(1/2)mn+(1/2)n².
∵m+n=mn=5,
∴原式=(1/2)(m²-mn+n²)=(1/2)[(m+n)²-3mn]=(1/2)(5²-3×5)=(1/2)×10=5.思路引导 解答本题先根据阴影部分的面积等于两个正方形的面积之和减去两个空白三角形的面积,再利用完全平方公式的变形求解代数式的值即可.
∵两个正方形边长分别为m,n,
∴阴影部分的面积为m²+n²-(1/2)m²-(1/2)(m+n)n=m²+n²-(1/2)m²-(1/2)mn-(1/2)n²=(1/2)m²-(1/2)mn+(1/2)n².
∵m+n=mn=5,
∴原式=(1/2)(m²-mn+n²)=(1/2)[(m+n)²-3mn]=(1/2)(5²-3×5)=(1/2)×10=5.思路引导 解答本题先根据阴影部分的面积等于两个正方形的面积之和减去两个空白三角形的面积,再利用完全平方公式的变形求解代数式的值即可.
15.已知$(x+m)(x-n)= x^{2}+7x-9$,则代数式$mn-m+n$的值为____.
答案:
2 [解析]
∵(x+m)(x-n)=x²+(m-n)x-mn=x²+7x-9,
∴m-n=7,mn=9,
∴mn-m+n=mn-(m-n)=9-7=2,
∴代数式mn-m+n的值为2.
∵(x+m)(x-n)=x²+(m-n)x-mn=x²+7x-9,
∴m-n=7,mn=9,
∴mn-m+n=mn-(m-n)=9-7=2,
∴代数式mn-m+n的值为2.
16.(2025·江苏南京鼓楼区期中)若$x-y= 3,xy= 5$,则$x^{2}+y^{2}= $____.
答案:
19 [解析]
∵(x-y)²=x²-2xy+y²=3²=9,
∴x²+y²-2×5=9,
∴x²+y²=19.
∵(x-y)²=x²-2xy+y²=3²=9,
∴x²+y²-2×5=9,
∴x²+y²=19.
17.(2024·四川巴中期末)计算$(-\frac {4}{5})^{2024}×(1.25)^{2023}×5$的值等于____.
答案:
4 [解析]原式=(-4/5×1.25)²⁰²³×(-4/5)×5=(-1)²⁰²³×(-4/5)×5=(-1)×(-4/5)×5=4.
18.中考新考法 新定义问题 定义:$\Phi [a,b,c]$是以a,b,c为系数的二次多项式,即$\Phi [a,b,c]= ax^{2}+bx+c$,其中a,b,c均为实数.例如$\Phi [1,2,3]= x^{2}+2x+3,\Phi [2,0,-2]= 2x^{2}-2$.①当$x= 2$时,求$\Phi [1,1,1]×\Phi [-1,-1,-1]= $____;②若$\Phi [p,q,-1]×\Phi [m,n,-2]= 2x^{4}+x^{3}-10x^{2}-x+2$,求$(4p-2q-1)(2m-n-1)= $____.
答案:
①-49 ②-6 [解析]①Φ[1,1,1]×Φ[-1,-1,-1]=(x²+x+1)×(-x²-x-1)=-(x²+x+1)².当x=2时,原式=-(2²+2+1)²=-49.②Φ[p,q,-1]×Φ[m,n,-2]=(px²+qx-1)×(mx²+nx-2)=pmx⁴+(pn+qm)x³+(-2p+qn-m)x²+(-n-2q)x+2=2x⁴+x³-10x²-x+2,
∴{pm=2,pn+qm=1,-2p+qn-m=-10,-n-2q=-1.}(4p-2q-1)(2m-n-1)=8pm-4pn-4p-4qm+2qn+2q-2m+n+1=8pm-4(pn+qm)+2(-2p+qn-m)-(-n-2q)+1=8×2-4×1+2×(-10)-(-1)+1=16-4-20+1+1=-6.
∴{pm=2,pn+qm=1,-2p+qn-m=-10,-n-2q=-1.}(4p-2q-1)(2m-n-1)=8pm-4pn-4p-4qm+2qn+2q-2m+n+1=8pm-4(pn+qm)+2(-2p+qn-m)-(-n-2q)+1=8×2-4×1+2×(-10)-(-1)+1=16-4-20+1+1=-6.
19.计算:
(1)$(x^{3})^{2}\cdot x^{2}-(-x)^{9}÷x$;
(2)$(x+1)(4x-2)-4(x+1)^{2}$;
(3)$(a+b)^{2}+(a+3b)(a-3b)$;
(4)$(3x^{2}y)^{3}\cdot (-2xy^{3}z)÷(-9x^{7}y^{5})$;
(5)$(-21x^{4}y^{3}-35x^{3}y^{2}+7x^{2}y^{2})÷(-7x^{2}y)$;
(6)$[(x+y)^{2}-y(2x+y)-8x]÷2x$.
(1)$(x^{3})^{2}\cdot x^{2}-(-x)^{9}÷x$;
(2)$(x+1)(4x-2)-4(x+1)^{2}$;
(3)$(a+b)^{2}+(a+3b)(a-3b)$;
(4)$(3x^{2}y)^{3}\cdot (-2xy^{3}z)÷(-9x^{7}y^{5})$;
(5)$(-21x^{4}y^{3}-35x^{3}y^{2}+7x^{2}y^{2})÷(-7x^{2}y)$;
(6)$[(x+y)^{2}-y(2x+y)-8x]÷2x$.
答案:
(1)原式=x⁶·x²+x⁹÷x=x⁸+x⁸=2x⁸.
(2)原式=4x²-2x+4x-2-4(x²+2x+1)=4x²-2x+4x-2-4x²-8x-4=-6x-6.
(3)原式=a²+2ab+b²+a²-9b²=2a²+2ab-8b².
(4)原式=27x⁶y³·(-2xy³z)÷(-9x⁷y⁵)=-54x⁷y⁶z÷(-9x⁷y⁵)=6yz.
(5)原式=21x⁴y³÷7x²y+35x³y²÷7x²y-7x²y²÷7x²y=3x²y²+5xy-y.
(6)原式=(x²+2xy+y²-2xy-y²-8x)÷2x=(x²-8x)÷2x=x/2-4.
(1)原式=x⁶·x²+x⁹÷x=x⁸+x⁸=2x⁸.
(2)原式=4x²-2x+4x-2-4(x²+2x+1)=4x²-2x+4x-2-4x²-8x-4=-6x-6.
(3)原式=a²+2ab+b²+a²-9b²=2a²+2ab-8b².
(4)原式=27x⁶y³·(-2xy³z)÷(-9x⁷y⁵)=-54x⁷y⁶z÷(-9x⁷y⁵)=6yz.
(5)原式=21x⁴y³÷7x²y+35x³y²÷7x²y-7x²y²÷7x²y=3x²y²+5xy-y.
(6)原式=(x²+2xy+y²-2xy-y²-8x)÷2x=(x²-8x)÷2x=x/2-4.
查看更多完整答案,请扫码查看


