22.(2025·福建厦门思明区期末)求值:$(2x+y)^{2}-(2x+y)(2x-y)-2y(x+y)$,其中$x= (\frac {1}{2})^{2024},y= -2^{2023}$.
答案:
原式=4x²+4xy+y²-(4x²-y²)-2xy-2y²=4x²+4xy+y²-4x²+y²-2xy-2y²=2xy.当x=(1/2)²⁰²⁴,y=-2²⁰²³时,原式=2×(1/2)²⁰²⁴×(-2²⁰²³)=1/2²⁰²⁴×(-2²⁰²⁴)=-1.
23.(2025·山东滨州博兴期末)(1)已知$2^{a}= m,3a= n$,试用含m,n的代数式表示$72^{a}$;
(2)已知$2a= m,2^{b}= n$,试用含m,n的代数式表示$8^{3a+2b}$;
(3)已知$2020^{x}= a,2020^{y}= b,2020^{z}= c$,试将$2020^{2016x+2018y-2068z}$用含a,b,c的代数式表示出来.
(2)已知$2a= m,2^{b}= n$,试用含m,n的代数式表示$8^{3a+2b}$;
(3)已知$2020^{x}= a,2020^{y}= b,2020^{z}= c$,试将$2020^{2016x+2018y-2068z}$用含a,b,c的代数式表示出来.
答案:
(1)
∵2a=m,3a=n,
∴原式=(2³×3²)ᵃ=(2ᵃ)³·(3ᵃ)²=m³n².
(2)
∵2ᵃ=m,2ᵇ=n,
∴原式=(2³)³ᵃ⁺²ᵇ=2⁹ᵃ⁺⁶ᵇ=(2ᵃ)⁹·(2ᵇ)⁶=m⁹n⁶.
(3)
∵2020ˣ=a,2020ʸ=b,2020ᶻ=c,
∴原式=(2020²⁰¹⁶ˣ·2020²⁰¹⁸ʸ)/2020²⁰⁸⁸ᶻ=(2020ˣ)²⁰¹⁶·(2020ʸ)²⁰¹⁸/(2020ᶻ)²⁰⁸⁸=(a²⁰¹⁶b²⁰¹⁸)/c²⁰⁸⁸.
(1)
∵2a=m,3a=n,
∴原式=(2³×3²)ᵃ=(2ᵃ)³·(3ᵃ)²=m³n².
(2)
∵2ᵃ=m,2ᵇ=n,
∴原式=(2³)³ᵃ⁺²ᵇ=2⁹ᵃ⁺⁶ᵇ=(2ᵃ)⁹·(2ᵇ)⁶=m⁹n⁶.
(3)
∵2020ˣ=a,2020ʸ=b,2020ᶻ=c,
∴原式=(2020²⁰¹⁶ˣ·2020²⁰¹⁸ʸ)/2020²⁰⁸⁸ᶻ=(2020ˣ)²⁰¹⁶·(2020ʸ)²⁰¹⁸/(2020ᶻ)²⁰⁸⁸=(a²⁰¹⁶b²⁰¹⁸)/c²⁰⁸⁸.
24.(2025·甘肃定西期末)完全平方公式:$(a\pm b)^{2}= a^{2}\pm 2ab+b^{2}$,经过适当的变形,可以解决很多的数学问题.例如:若$(2023-x)(x-2018)= 4$,求$(2023-x)^{2}+(x-2018)^{2}$的值.解:设$2023-x= a,x-2018= b$,则$(2023-x)(x-2018)= ab= 4,a+b= (2023-x)+(x-2018)= 5$,所以$(2023-x)^{2}+(x-2018)^{2}= a^{2}+b^{2}= (a+b)^{2}-2ab= 5^{2}-2×4= 17$.根据上面的解题思路与方法,解决下列问题:
(1)填空:若$x+y= 10,xy= 2,x^{2}+y^{2}= $____;
(2)$x+y= 10,x^{2}+y^{2}= 52,xy= $____;
(3)若$(4+x)(5-x)= 8$,则$(4+x)^{2}+(5-x)^{2}= $____;
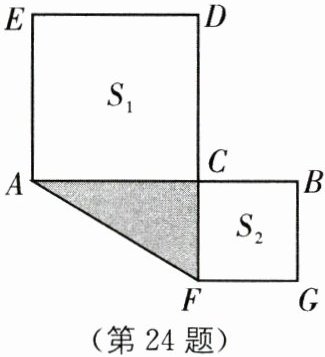
(4)如图,C是线段AB上的一点,分别以AC,BC为边向两边作正方形,设$AB= 8$,两正方形的面积和$S_{1}+S_{2}= 48$,求图中阴影部分面积.
(1)填空:若$x+y= 10,xy= 2,x^{2}+y^{2}= $____;
(2)$x+y= 10,x^{2}+y^{2}= 52,xy= $____;
(3)若$(4+x)(5-x)= 8$,则$(4+x)^{2}+(5-x)^{2}= $____;
(4)如图,C是线段AB上的一点,分别以AC,BC为边向两边作正方形,设$AB= 8$,两正方形的面积和$S_{1}+S_{2}= 48$,求图中阴影部分面积.

答案:
(1)96 [解析]
∵x+y=10,xy=2,
∴x²+y²=(x+y)²-2xy=10²-4=96.
(2)24 [解析]
∵x+y=10,x²+y²=52,
∴2xy=(x+y)²-(x²+y²)=10²-52=48,
∴xy=24.
(3)65 [解析]设4+x=s,5-x=t,
∴s+t=4+x+5-x=9,st=(4+x)(5-x)=8,
∴s²+t²=(s+t)²-2st=9²-2×8=65,
∴(4+x)²+(5-x)²=s²+t²=65.
(4)设AC=c,BC=d,
∴AB=AC+BC=c+d=8,AC²+BC²=c²+d²=S₁+S₂=48,
∴2cd=(c+d)²-(c²+d²)=8²-48=16,
∴cd=8,
∴AC·BC=8,
∴S_阴影=(1/2)AC·CF=(1/2)AC·BC=4.
(1)96 [解析]
∵x+y=10,xy=2,
∴x²+y²=(x+y)²-2xy=10²-4=96.
(2)24 [解析]
∵x+y=10,x²+y²=52,
∴2xy=(x+y)²-(x²+y²)=10²-52=48,
∴xy=24.
(3)65 [解析]设4+x=s,5-x=t,
∴s+t=4+x+5-x=9,st=(4+x)(5-x)=8,
∴s²+t²=(s+t)²-2st=9²-2×8=65,
∴(4+x)²+(5-x)²=s²+t²=65.
(4)设AC=c,BC=d,
∴AB=AC+BC=c+d=8,AC²+BC²=c²+d²=S₁+S₂=48,
∴2cd=(c+d)²-(c²+d²)=8²-48=16,
∴cd=8,
∴AC·BC=8,
∴S_阴影=(1/2)AC·CF=(1/2)AC·BC=4.
查看更多完整答案,请扫码查看


