《2025年实验班提优训练八年级数学上册人教版》

1.(2025·四川泸州期中)计算$(-2a^{2})^{3}$的结果正确的是( ).

A.$-2a^{6}$
B.$-6a^{8}$
C.$-8a^{6}$
D.$-8a^{3}$

答案： C [解析](-2a²)³=-8a⁶.故选C.

2.(2024·四川南充期末)已知$a-b= 1$,则$a^{2}-b^{2}-2b$的值为( ).

A.4
B.3
C.1
D.0

答案： C [解析]
∵a-b=1,
∴a=b+1,
∴a²-b²-2b=(b+1)²-b²-2b=b²+2b+1-b²-2b=1.故选C.

3.(2025·重庆巴南区期末)若$4y^{2}-my+16$可以配成一个完全平方公式,则m的值为( ).

A.-8
B.$\pm 8$
C.16
D.$\pm 16$

答案： D [解析]
∵4y²-my+16可配成一个完全平方式,
∴-my=±2·2y·4,解得m=±16.故选D.

4.(2024·达州中考)下列计算正确的是( ).

A.$a^{2}+a^{3}= a^{5}$
B.$(a+2)^{2}= a^{2}+2a+4$
C.$(-2a^{2}b^{3})^{3}= -8a^{6}b^{9}$
D.$a^{12}÷a^{6}= a^{2}$

答案： C [解析]a²+a³不能化简,故A选项错误;(a+2)²=a²+4a+4,故B选项错误;(-2a²b³)³=-8a⁶b⁹,故C选项正确;a¹²÷a⁶=a⁶,故D选项错误.故选C.

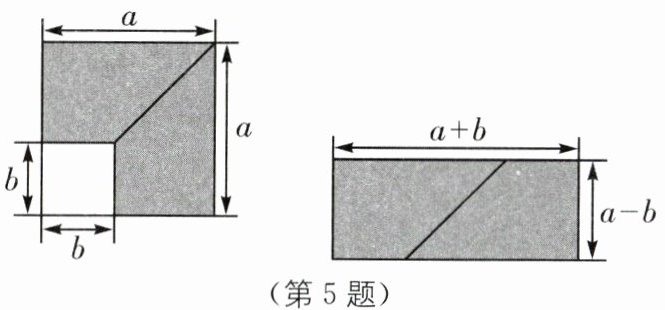
5.(2025·安徽阜阳期末)按如图所示的方式分割的正方形,再拼接成长方形的方案中,可以验证的等式是( ).

A.$(a+b)^{2}= a^{2}+2ab+b^{2}$
B.$(a-b)^{2}= a^{2}-2ab+b^{2}$
C.$(a-b)^{2}= (a+b)^{2}-4ab$
D.$a^{2}-b^{2}= (a+b)(a-b)$

答案： D [解析]左边一幅图阴影部分面积为a²-b²,右边一幅图阴影部分面积为(a+b)(a-b).
∵两幅图阴影部分面积相等,
∴a²-b²=(a+b)(a-b).故选D.解题思路 分别表示出两幅图中阴影部分的面积,再根据两幅图阴影部分面积相等即可得答案.

6.(2025·四川成都锦江区期末)已知$m^{x}= 2,m^{y}= 5$,则$m^{2x+y}$值为( ).

A.9
B.20
C.$4^{5}$
D.$m^{9}$

答案： B [解析]
∵mˣ=2,mʸ=5,
∴m²ˣ⁺ʸ=m²ˣ·mʸ=(mˣ)²·mʸ=2²×5=4×5=20.故选B.

7.(2025·重庆万州区期末)若$(2x+m)(x-4)$的展开式中不含x项,则实数m的值为( ).

A.-8
B.0
C.4
D.8

答案： D [解析]
∵(2x+m)(x-4)=2x²-8x+mx-4m=2x²+(m-8)x-4m,展开式中不含x项,
∴m-8=0,即m=8.故选D.思路引导 解答本题先根据多项式乘多项式展开式子,合并同类项,不含x项,就是x项系数为0,进而求出m的值.

8.我们知道,引进了无理数后,有理数集就扩展到实数集;同样,如果引进“虚数”,实数集就扩展到“复数集”.现在我们定义“虚数单位”,其运算规则是：$i^{1}= i,i^{2}= -1,i^{3}= -i,i^{4}= 1,i^{5}= i,i^{6}= -1,i^{7}= -i$,则$i^{2025}$的值是( ).

A.1
B.-1
C.i
D.-i

答案： C [解析]
∵i¹=i,i²=-1,i³=-i,i⁴=1,i⁵=i,i⁶=-1,i⁷=-i,…,每4个数据一循环.
∵2025÷4=506……1,
∴i²⁰²⁵=i.故选C.

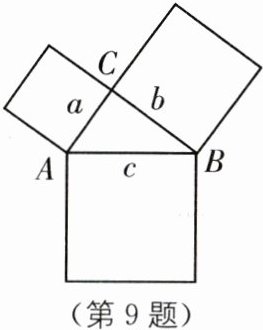
9.(2025·上海宝山区期末)根据整式与整式相乘,可以得到等式:$(x+y+z)^{2}= x^{2}+y^{2}+z^{2}+2xy+2xz+2yz$.试利用这个等式解决以下问题:如图,在$△ABC$中,$∠C= 90^{\circ }$,分别以AC,BC,AB为边向外侧作正方形.如果AC,BC,AB的长分别是a,b,c,且$a+b+c= 12,ab+ac+bc= 37$,那么这三个正方形的面积和是( ).

A.70
B.107
C.60
D.83

答案： A [解析]由题意,可得(a+b+c)²=a²+b²+c²+2ab+2ac+2bc.
∵a+b+c=12,ab+ac+bc=37,
∴12²=a²+b²+c²+2×37,
∴a²+b²+c²=144-74=70,即这三个正方形的面积和是70.故选A.