《2025年实验班提优训练八年级数学上册人教版》

21.(1)如图(1),$∠A= 90^{\circ }$,请用直尺和圆规作一条直线,把$△ABC$分割成两个等腰三角形(不写作法,但须保留作图痕迹).
(2)已知内角度数的两个三角形如图(2)、图(3)所示.请你判断,能否分别画一条直线把它们分割成两个等腰三角形?若能,请画出直线,并标注底角的度数.
(3)一个三角形有一内角为$48^{\circ }$,如果经过其一个顶点作直线能把其分成两个等腰三角形,那么它的最大内角质值为____.

答案：

(1)如图
(1),作BA的垂直平分线交BC于点E,连接
AE,则直线AE即为所求.
　　　　　　　
(2)能.如图
(2)
(3):
　　　　　　　

(3)108°或90°或99°或88°或116°

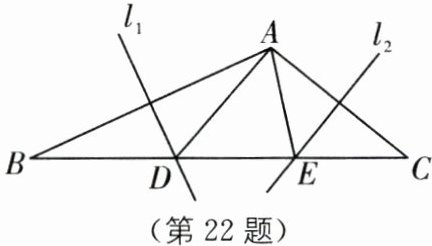
22.(2025·江苏苏州期末)如图,在$△ABC$中,边AB的垂直平分线$l_{1}$与边BC相交于点D,边AC的垂直平分线$l_{2}$与边BC相交于点E(D在E的左侧).若$△ADE$的周长为8,$∠DAE= 60^{\circ }$.
(1)求BC的长;
(2)求$∠BAC$的度数.

答案：
(1)
∵l₁垂直平分AB,
∴DB=DA,同理EA=EC.
∵△ADE的周长为AD+AE+DE=8,
∴BC=BD+DE+EC=DA+DE+EA=8.
(2)
∵∠DAE=60°,
∴∠ADE+∠AED=180°−60°=120°.
∵DA=DB,EA=EC,
∴∠BAD=∠ABC,∠EAC=∠ACB.
∵∠ADE=∠BAD+∠ABC,∠AED=∠EAC+∠ACB,
∴∠BAD+∠EAC=$\frac{1}{2}$(∠ADE+∠AED)=60°,
∴∠BAC=60°+60°=120°.

23.(2025·河南洛阳伊川期末)[问题发现]我们知道“线段垂直平分线上的点到线段两端的距离相等”,那么不在线段垂直平分线上的点到线段两端的距离大小如何判断呢?
[自主研究]
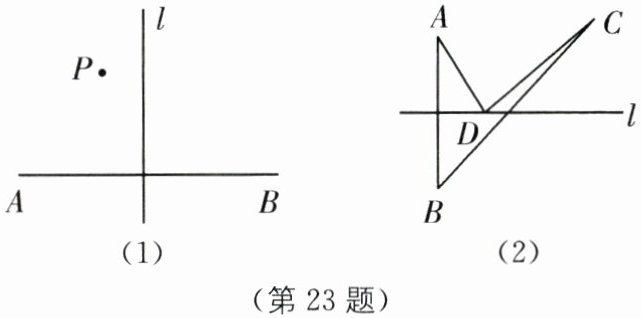
(1)如图(1),直线l是线段AB的垂直平分线,点P在直线l的左侧,经测量,$PA＜PB$,请证明这个结论;
[迁移研究]
(2)如图(2),直线l是线段AB的垂直平分线,点C在直线l外,且与点A在直线l的同侧,点D是直线l上的任意一点,连接AD,BC,CD,试判断BC和$AD+CD$之间的大小关系,并说明理由.

答案：

(1)如图
(1),连接PA,PB,AM.
∵直线l是线段AB的垂直平分线,
∴AM=BM,
∴PB=PM+MB=PM+AM;
∵PM+AM＞PA,
∴PA＜PB.
(2)如图
(2),AD+CD≥BC,理由如下:
　　当D不在线段BC上时，连接BD.
∵直线l是线段AB的垂直平分线，
∴AD=BD.
∵BD+CD＞BC,
∴AD+CD＞BC.
　　当D在线段BC上时,AD+CD=BC.
　　综上所述,AD+CD≥BC.