《2025年实验班提优训练八年级数学上册人教版》

25. 如图,$AD为△ABC$的角平分线.
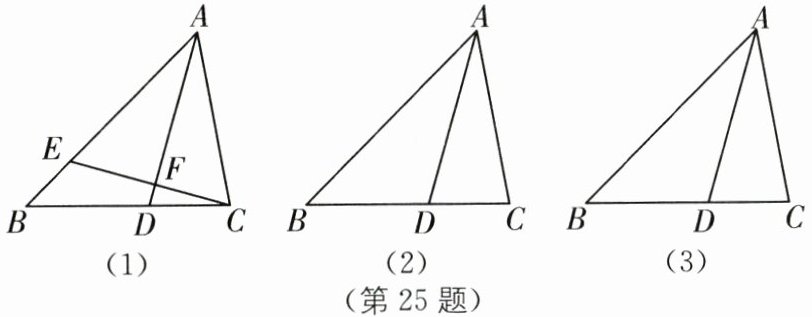
(1)如图(1),若$CE⊥AD于点F$,交$AB于点E,AB= 7,AC= 5$,则$BE= $____;
(2)如图(2),若$AB= 7,AC= 5,△ACD$的面积是10,求$△ABC$的面积;
(3)如图(3),若$∠C= 2∠B,AB= m,AC= n$,请直接写出$BD$的长(用含$m,n$的式子表示).

答案：
(1)2　[解析]
∵AD是△ABC的角平分线，
∴∠BAD=∠CAD.
∵CE⊥AD,
∴∠CFA=∠EFA.在△AEF和△ACF中,∠EAF=∠CAF,AF=AF,∠AFE=∠AFC,
∴△AEF≌△ACF(ASA),
∴AE=AC.
∵AB=7,AC=5,
∴BE=AB−AE=AB−AC=7−5=2.
(2)如图
(1),过点D作DE⊥AC于点E,DF⊥AB于点F,
∵AD为△ABC的角平分线,
∴DF=DE.
∵AC=5,△ACD的面积是10,
∴DE=4,
∴DF=4,
∴S△ABD=$\frac{1}{2}$AB·DF=$\frac{1}{2}$×7×4=14,
∴S△ABC=S△ABD+S△ACD=14+10=24.
(3)如图
(2),在AB上取AN=AC,
∵AD是△ABC的平分线,
∴∠NAD=∠CAD.在△ADN和△ADC中,AN=AC,∠NAD=∠CAD,AD=AD,
∴△ADN≌△ADC(SAS),
∴∠AND=∠C,DN=CD.
∵∠C=2∠B,
∴∠AND=2∠B.又∠AND=∠B+∠BDN,
∴∠B=∠BDN,
∴BN=DN=AB−AN=AB−AC.
∵AB=m,AC=n,
∴CD=DN=BN=m−n,根据△ABD边AB上的高和△ACD边AC上的高相等，
∴面积比等于$\frac{AB}{AC}$,又BD和CD上的高相等，
∴面积比等于$\frac{BD}{CD}$,可得$\frac{BD}{CD}$=$\frac{AB}{AC}$,
∴$\frac{BD}{m−n}$=$\frac{m}{n}$,
∴BD=$\frac{m}{n}$(m−n).

26. 为了解决一些较为复杂的数学问题,我们常常采用从特殊到一般的思想,先从特殊的情形入手,从中找到解决问题的方法.
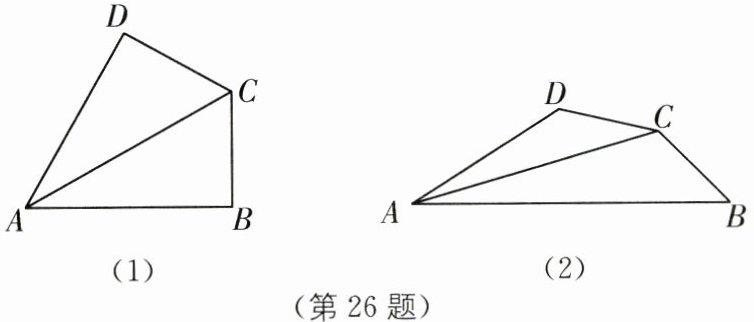
已知:在四边形$ABCD$中,$AC平分∠BAD,∠B+∠D= 180^{\circ}$.
(1)如图(1),当$∠B= 90^{\circ}$时,求证:$CB= CD$.
(2)如图(2),当$∠B＜90^{\circ}$时.
①求证:$CB= CD$;
②若$AB= 10cm,AD= 6cm,∠B= 45^{\circ}$,则点$C到AB$的距离是____$cm$.

答案：
(1)
∵∠B+∠D=180°,∠B=90°,
∴∠D=90°.
∵AC平分∠BAD,
∴∠CAD=∠CAB.
∵AC=AC,
∴△ACD≌△ACB(AAS),
∴CD=BC.
(2)①如图,过点C作CE⊥BA于点E,过点C作CF⊥AD交AD延长线于点F.
∵CF⊥AD,CE⊥AB,
∴∠F=∠AEC=90°.
∵AC平分∠BAD,
∴∠CAF=∠CAE.又AC=AC,
∴△ACE≌△ACF(AAS).
∴CE=CF.
∵∠B+∠ADC=180°,∠ADC+∠FDC=180°,
∴∠B=∠FDC.
∵∠CEB=∠F=90°,CE=CF,
∴△CBE≌△CDF(AAS),
∴BC=CD.②2　[解析]由①可知△ACF≌△ACE,△CDF≌△CBE,
∴AF=AE,DF=BE,
∴AD+DF=AB−BE,即AD+BE=AB−BE.
∴2BE=AB−AD.
∵AB=10cm,AD=6cm,
∴BE=2cm.
∵∠B=45°,
∴△BCE为等腰直角三角形，
∴CE=BE=2cm,
∴点C到AB的距离是2cm.