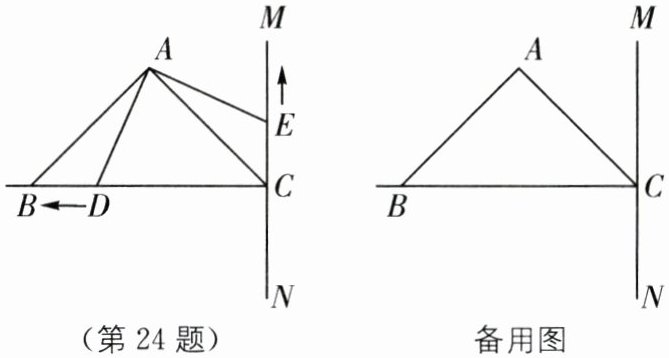
24.如图,在$△ABC$中,$AB= AC,∠BAC= 90^{\circ },BC= 6$厘米,过点C作直线$MN⊥BC$,动点D从点C开始沿射线CB方向以每秒2厘米的速度运动,动点E也同时从点C开始在直线MN上以每秒1厘米的速度向远离点C的方向运动,分别连接AD,AE,设运动时间为$t(t>0)$秒.
(1)$CE= $____,$CD= $____,$BD= $____(用含有t的式子表示).
(2)当点D在线段BC上,且$AD⊥AE$时,$△ABD是否与△ACE$全等?说明理由;此时$CE+CD= $____.
(3)当点D在线段CB的延长线上,且$AD⊥AE$时,CE与CD有何数量关系?说明理由.
备用图
(1)$CE= $____,$CD= $____,$BD= $____(用含有t的式子表示).
(2)当点D在线段BC上,且$AD⊥AE$时,$△ABD是否与△ACE$全等?说明理由;此时$CE+CD= $____.
(3)当点D在线段CB的延长线上,且$AD⊥AE$时,CE与CD有何数量关系?说明理由.

备用图
答案:
(1)t厘米 2t厘米 |6−2t|厘米
(2)BC(或6厘米) △ABD≌△ACE,理由如下:
∵AB=AC,∠BAC=90°,MN⊥BC,
∴∠ABC=∠ACB=45°,∠MCD=90°,
∴∠ACE=45°=∠ABC.
∵AD⊥AE,
∴∠DAE=90°=∠BAC,
∴∠BAD=∠CAE,
∴△ABD≌△ACE(ASA),
∴BD=CE,
∴CE+CD=BD+CD=BC=6厘米.
(3)CD−CE=6厘米.理由如下:如图

∵AB=AC,∠BAC=90°,MN⊥BC,
∴∠ABC=∠ACB=45°,∠BCN=90°,
∴∠ABD=135°=∠ACE.
∵AD⊥AE,
∴∠DAE=90°=∠BAC,
∴∠BAD=∠CAE,
∴△ABD≌△ACE(ASA),
∴BD=CE,
∴CD−CE=CD−BD=BC=6厘米,
解后反思 本题是三角形综合题,考查了全等三角形的判定和性质,等腰直角三角形的性质等知识,灵活运用这些性质解决问题是解题的关键,
(1)t厘米 2t厘米 |6−2t|厘米
(2)BC(或6厘米) △ABD≌△ACE,理由如下:
∵AB=AC,∠BAC=90°,MN⊥BC,
∴∠ABC=∠ACB=45°,∠MCD=90°,
∴∠ACE=45°=∠ABC.
∵AD⊥AE,
∴∠DAE=90°=∠BAC,
∴∠BAD=∠CAE,
∴△ABD≌△ACE(ASA),
∴BD=CE,
∴CE+CD=BD+CD=BC=6厘米.
(3)CD−CE=6厘米.理由如下:如图

∵AB=AC,∠BAC=90°,MN⊥BC,
∴∠ABC=∠ACB=45°,∠BCN=90°,
∴∠ABD=135°=∠ACE.
∵AD⊥AE,
∴∠DAE=90°=∠BAC,
∴∠BAD=∠CAE,
∴△ABD≌△ACE(ASA),
∴BD=CE,
∴CD−CE=CD−BD=BC=6厘米,
解后反思 本题是三角形综合题,考查了全等三角形的判定和性质,等腰直角三角形的性质等知识,灵活运用这些性质解决问题是解题的关键,
25.(2025·浙江台州路桥区期末)尺规作图问题:
已知:$∠AOB$,求作:$∠AOB$的平分线.
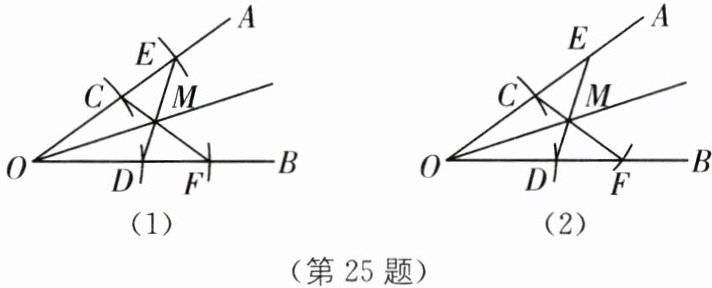
小聪的作法:如图(1),以点O为圆心,任意长为半径画弧,交OA,OB于点C,D,再以点O为圆心,大于OC长为半径画弧,交OA,OB于点E,F.连接CF,DE,交于点M,画射线OM,则射线OM即为所求.
小慧的作法:如图(2),以点O为圆心,任意长为半径画弧,交OA,OB于点C,D,在OA上任取一点E,再以点C为圆心,DE长为半径画弧,交OB于点F,连接CF,DE,交于点M,画射线OM,则射线OM即为所求.老师的观点:小聪的作法是正确的,小慧的作法不一定正确.
(1)如图(1),证明OM平分$∠AOB$;
(2)如图(2),说明小慧的作法中可能存在的问题.
已知:$∠AOB$,求作:$∠AOB$的平分线.
小聪的作法:如图(1),以点O为圆心,任意长为半径画弧,交OA,OB于点C,D,再以点O为圆心,大于OC长为半径画弧,交OA,OB于点E,F.连接CF,DE,交于点M,画射线OM,则射线OM即为所求.
小慧的作法:如图(2),以点O为圆心,任意长为半径画弧,交OA,OB于点C,D,在OA上任取一点E,再以点C为圆心,DE长为半径画弧,交OB于点F,连接CF,DE,交于点M,画射线OM,则射线OM即为所求.老师的观点:小聪的作法是正确的,小慧的作法不一定正确.
(1)如图(1),证明OM平分$∠AOB$;
(2)如图(2),说明小慧的作法中可能存在的问题.

答案:
(1)由作图步骤可知,OC=OD,OE=OF.
OC=OD,
在△COF和△DOE中,∠COF=∠DOE,
OF=OE,
{
∴△COF≌△DOE(SAS),
∴∠OFC=∠OED.
∵OC=OD,OE=OF,
∴OE−OC=OF−OD,
∴CE=DF.
∠CEM=∠DFM,
在△CME和△DMF中,∠CME=∠DMF,
CE=DF,
{
∴△CME≌△DMF(AAS),
∴ME=MF.
OE=OF,
在△OME和△OMF中,ME=MF,
OM=OM,
{
∴△OME≌△OMF(SSS),
∴∠EOM=∠FOM,即OM为∠AOB的平分线.
(2)如图,

小慧的作法中,以点C为圆心,DE长为半径画弧,交OB 于点F,可能有两个交点:F,F',得到的△COF不唯一,不能证明△COF≌△DOE.
(1)由作图步骤可知,OC=OD,OE=OF.
OC=OD,
在△COF和△DOE中,∠COF=∠DOE,
OF=OE,
{
∴△COF≌△DOE(SAS),
∴∠OFC=∠OED.
∵OC=OD,OE=OF,
∴OE−OC=OF−OD,
∴CE=DF.
∠CEM=∠DFM,
在△CME和△DMF中,∠CME=∠DMF,
CE=DF,
{
∴△CME≌△DMF(AAS),
∴ME=MF.
OE=OF,
在△OME和△OMF中,ME=MF,
OM=OM,
{
∴△OME≌△OMF(SSS),
∴∠EOM=∠FOM,即OM为∠AOB的平分线.
(2)如图,

小慧的作法中,以点C为圆心,DE长为半径画弧,交OB 于点F,可能有两个交点:F,F',得到的△COF不唯一,不能证明△COF≌△DOE.
查看更多完整答案,请扫码查看


