搜索
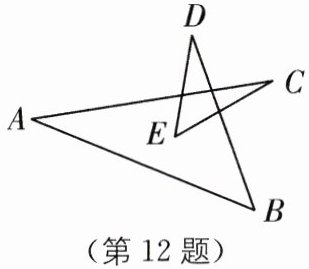
12. 转化思想 (2024·河南漯河实验中学期中)图中$∠A+∠B+∠C+∠D+∠E= $______$^{\circ }$.
答案：
180 [解析]如图，连接CD，设AC，BD交于点F，
∵∠A+∠B+∠AFB=∠CDF+∠DCF+∠CFD=180°，∠AFB=∠CFD，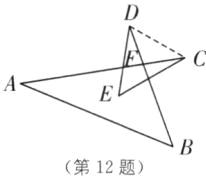
∴∠A+∠B=∠CDF+∠DCF，
∴∠A+∠B+∠ACE+∠BDE+∠E=∠CDF+∠DCF+∠FCE+∠FDE+∠E=180°.
180 [解析]如图，连接CD，设AC，BD交于点F，
∵∠A+∠B+∠AFB=∠CDF+∠DCF+∠CFD=180°，∠AFB=∠CFD，
∴∠A+∠B=∠CDF+∠DCF，
∴∠A+∠B+∠ACE+∠BDE+∠E=∠CDF+∠DCF+∠FCE+∠FDE+∠E=180°.
13. 在平面直角坐标系中,点$A(-5,-8)关于y$轴的对称点的坐标是______.
答案：
(5，−8) [解析]在平面直角坐标系中，点A(−5，−8)关于y轴的对称点的坐标是(5，−8).
14. (2025·广东云浮罗定期末)如图,$\triangle ABC中∠BAC的外角的平分线AE与∠ABC的平分线BD相交于点P,∠C= 80^{\circ }$,则$∠APB$的度数是______.
答案：
40° [解析]
∵BP平分∠ABC，AP平分∠CAM，
∴∠ABP=$\frac{1}{2}$∠ABC，∠MAP=$\frac{1}{2}$∠CAM.
∵∠MAP=∠ABP+∠APB，
∴$\frac{1}{2}$∠CAM=$\frac{1}{2}$∠ABC+∠APB，
∴$\frac{1}{2}$(∠ABC+∠C)=$\frac{1}{2}$∠ABC+∠APB，
∴∠APB=$\frac{1}{2}$∠C=$\frac{1}{2}$×80°=40°.
∵BP平分∠ABC，AP平分∠CAM，
∴∠ABP=$\frac{1}{2}$∠ABC，∠MAP=$\frac{1}{2}$∠CAM.
∵∠MAP=∠ABP+∠APB，
∴$\frac{1}{2}$∠CAM=$\frac{1}{2}$∠ABC+∠APB，
∴$\frac{1}{2}$(∠ABC+∠C)=$\frac{1}{2}$∠ABC+∠APB，
∴∠APB=$\frac{1}{2}$∠C=$\frac{1}{2}$×80°=40°.
15. (2024·枣庄滕州模拟)在同一平面内,将一副直角三角板$ABC和EDF如图放置(∠C= 60^{\circ },∠F= 45^{\circ })$,其中直角顶点$D是BC$的中点,点$A在DE$上,则$∠CGF= $______$^{\circ }$.
答案：
15
16. (2025·北京十一中期中)在等边三角形$ABC$中,$M,N,P分别是边AB,BC,CA$上的点(不与端点重合),对于任意等边三角形$ABC$,下面四个结论中所有正确结论的序号是______.
①存在无数个$\triangle MNP$是等腰三角形;
②只存在一个$\triangle MNP$是等边三角形;
③存在无数个$\triangle MNP$是等腰直角三角形;
④存在一个$\triangle MNP在所有\triangle MNP$中面积最小.
①存在无数个$\triangle MNP$是等腰三角形;
②只存在一个$\triangle MNP$是等边三角形;
③存在无数个$\triangle MNP$是等腰直角三角形;
④存在一个$\triangle MNP在所有\triangle MNP$中面积最小.
答案：
①③ [解析]如图
(1)，当AM=BN=PC时，可证△PMN是等边三角形，这样的三角形有无数个.
如图
(2)，当NM=NP，∠MNP=90°时，△MNP是等腰直角三角形，这样的三角形有无数个(见图
(3)).
△PNM的面积不存在最小值(面积可以接近0，没有最小值).
①③ [解析]如图
(1)，当AM=BN=PC时，可证△PMN是等边三角形，这样的三角形有无数个.
如图(2)，当NM=NP，∠MNP=90°时，△MNP是等腰直角三角形，这样的三角形有无数个(见图
(3)).
△PNM的面积不存在最小值(面积可以接近0，没有最小值). 17. (2025·湖南衡阳来阳期末)如图,在四边形$ABCD$中,$AD// BC$.若$∠DAB的平分线AE交CD于点E$,连接$BE$,且$BE平分∠ABC$,得到如下结论:①$∠AEB= 90^{\circ }$;②$BC+AD= AB$;③$BE= \frac {1}{2}CD$;④$BC= CE$,那么以上结论正确的是______.(填序号)
答案：
①② [解析]
∵在四边形ABCD中，AD//BC，
∴∠DAB+∠ABC=180°.
∵∠DAB的平分线AE交CD于E，BE平分∠ABC，
∴∠DAB=2∠BAE=2∠DAE，∠ABC=2∠ABE=2∠CBE，
∴2∠BAE+2∠ABE=180°，
∴∠BAE+∠ABE=90°，
∴∠AEB=180°−(∠BAE+∠ABE)=90°，故①正确；如图，延长AE与BC的延长线交于点F，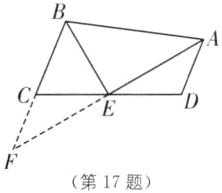
∵AD//BC，
∴∠F=∠EAD，
∴∠F=∠EAB，
∴BF=BA.
∵BE平分∠ABC，
∴BE垂直平分AF，
∴AE=EF.在△FEC和△AED中，{∠FEC=∠AED，EF=AE，∠F=∠EAD，
∴△FEC≌△AED(ASA)，
∴FC=AD，CE=DE，即CE=$\frac{1}{2}$CD，
∴BC+AD=BC+CF=AB，故②正确；
∵BE与CE不一定相等，
∴BE=$\frac{1}{2}$CD不一定成立，故③错误；
∵AB与CD不一定平行，
∴∠ABE与∠BEC不一定相等，即∠CBE与∠BEC不一定相等，
∴BC与CE不一定相等，故④错误.综上，正确的是①②.
①② [解析]
∵在四边形ABCD中，AD//BC，
∴∠DAB+∠ABC=180°.
∵∠DAB的平分线AE交CD于E，BE平分∠ABC，
∴∠DAB=2∠BAE=2∠DAE，∠ABC=2∠ABE=2∠CBE，
∴2∠BAE+2∠ABE=180°，
∴∠BAE+∠ABE=90°，
∴∠AEB=180°−(∠BAE+∠ABE)=90°，故①正确；如图，延长AE与BC的延长线交于点F，
∵AD//BC，
∴∠F=∠EAD，
∴∠F=∠EAB，
∴BF=BA.
∵BE平分∠ABC，
∴BE垂直平分AF，
∴AE=EF.在△FEC和△AED中，{∠FEC=∠AED，EF=AE，∠F=∠EAD，
∴△FEC≌△AED(ASA)，
∴FC=AD，CE=DE，即CE=$\frac{1}{2}$CD，
∴BC+AD=BC+CF=AB，故②正确；
∵BE与CE不一定相等，
∴BE=$\frac{1}{2}$CD不一定成立，故③错误；
∵AB与CD不一定平行，
∴∠ABE与∠BEC不一定相等，即∠CBE与∠BEC不一定相等，
∴BC与CE不一定相等，故④错误.综上，正确的是①②.
18. 如图,在$\triangle ABC$中,$AB= 20cm,AC= 12cm$,点$P从点B出发以每秒3cm的速度向点A$运动,点$Q从点A同时出发以每秒2cm的速度向点C$运动,其中一个动点到达端点,另一个动点也随之停止,当$\triangle APQ是以PQ$为底的等腰三角形时,运动的时间是______秒.
答案：
4 [解析]设运动的时间为x，在△ABC中，AB=20cm，AC=12cm，点P从点B出发以每秒3cm的速度向点A运动，点Q从点A同时出发以每秒2cm的速度向点C运动，当△APQ是以PQ为底的等腰三角形时，AP=AQ，AP=20−3x，AQ=2x，即20−3x=2x，解得x=4.
19. 如图,已知$D是BC$上一点,$AB= BD,DE// AB,∠A= ∠DBE$.
求证:$AC= BE$.
求证:$AC= BE$.
答案：
∵DE//AB，
∴∠EDB=∠CBA.又∠A=∠DBE，AB=BD，
∴△ABC≌△BDE(ASA).
∴AC=BE.
∵DE//AB，
∴∠EDB=∠CBA.又∠A=∠DBE，AB=BD，
∴△ABC≌△BDE(ASA).
∴AC=BE.
查看更多完整答案，请扫码查看
