《2025年暑假作业及活动新疆文化出版社八年级数学》

6. 今有长度分别为5厘米、9厘米、12厘米、13厘米、16厘米、20厘米的6种木条,要制成型号、大小不同的直角三角板,制法有()
A. 2种
B. 3种
C. 4种
D. 5种

答案： A

1. 如图2,$AD为\triangle ABC$的高,$AB= 10$,$AD= 8$,$BC= 12$,试说明$\triangle ABC$为等腰三角形。

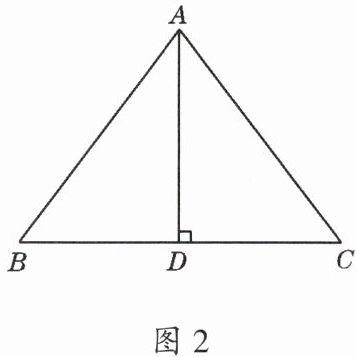
答案： 由$AB^{2}=AD^{2}+BD^{2}$得$BD=6$，$DC=6$，再证$\triangle ABD\cong\triangle ACD$

2. 如图3,已知四边形$ABCD$中,$AB$、$BC$、$CD$、$DA的长分别为8$、$6$、$26$、$24$,$\angle ABC= 90^{\circ}$,求$S_{四边形ABCD}$。

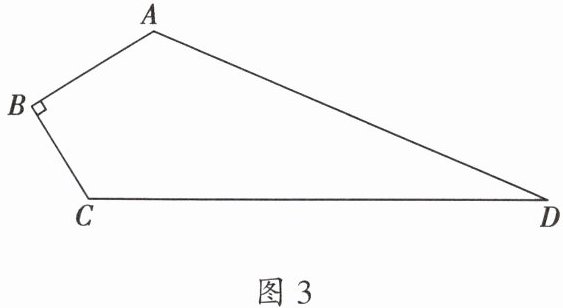
答案： 连接$AC$，由$AB^{2}+BC^{2}=AC^{2}$得$AC=10$，由$AC^{2}+AD^{2}=CD^{2}$得$\triangle ACD$为直角三角形，求出$S_{ABCD}=144$