第8页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
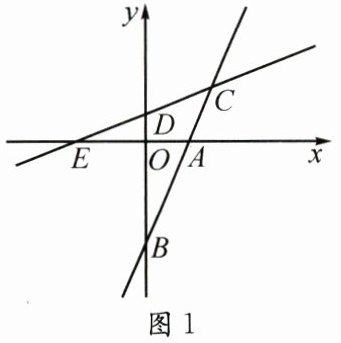
26. (12 分)如图 1,在平面直角坐标系中,直线 $y = 2x + b$ 与 $x$ 轴、$y$ 轴分别交于点 $A$,$B$,$S_{\triangle AOB} = 4$,$C(3,m)$ 是直线 $AB$ 上一点,在直线 $AB$ 左侧过点 $C$ 的直线交 $y$ 轴于点 $D$,交 $x$ 轴于点 $E$.
(1) 求 $m$ 和 $b$ 的值;
(2) 当 $\angle ACD = 45^{\circ}$ 时,求直线 $CD$ 的解析式;
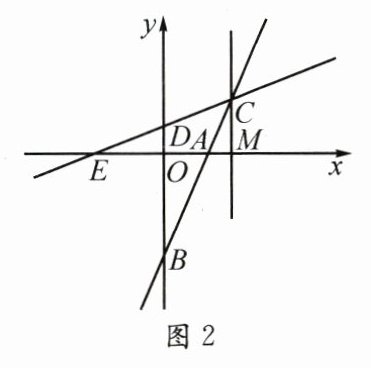
(3) 如图 2,在(2)的条件下,过点 $C$ 作 $CM \perp x$ 轴,在直线 $AC$ 上一点 $P$,直线 $CD$ 上一点 $Q$,直线 $CM$ 上一点 $H$,当四边形 $AHQP$ 为菱形时,求点 $P$ 的坐标.
(1) 求 $m$ 和 $b$ 的值;
(2) 当 $\angle ACD = 45^{\circ}$ 时,求直线 $CD$ 的解析式;
(3) 如图 2,在(2)的条件下,过点 $C$ 作 $CM \perp x$ 轴,在直线 $AC$ 上一点 $P$,直线 $CD$ 上一点 $Q$,直线 $CM$ 上一点 $H$,当四边形 $AHQP$ 为菱形时,求点 $P$ 的坐标.


答案:
【解】
(1)
∵直线 $y = 2x + b$ 与 $x$ 轴、$y$ 轴分别交于点 $A$,$B$,
∴$B(0,b)$,$A(-\frac{b}{2},0)$。
∵$S_{\triangle AOB}=\frac{1}{2}OA\cdot OB = 4$,
∴$\frac{1}{2}\times(-\frac{b}{2})\times(-b) = 4$,解得 $b = -4$ 或 $b = 4$ (舍去),
∴$b$ 的值为 $-4$,
∴直线 $AB$ 的解析式为 $y = 2x + b = 2x - 4$。
∵$C(3,m)$ 是直线 $AB$ 上一点,
∴$m = 2\times3 - 4 = 2$。
(2)
∵$b$ 的值为 $-4$,$m$ 的值为 $2$,
∴$B(0,-4)$,$A(2,0)$,$C(3,2)$。
如图 1,过点 $A$ 作 $AM\perp CD$ 于点 $M$,过点 $M$ 作 $MR\perp x$ 轴于点 $R$,过点 $C$ 作 $CT\perp MR$ 于点 $T$,设 $M(q,n)$。

∴$\angle ARM=\angle MTC = 90^{\circ}$,$\angle AMC = 90^{\circ}$。
∵$\angle ACD = 45^{\circ}$,$\angle AMR+\angle MAR=\angle AMR+\angle CMT = 90^{\circ}$,
∴$\angle ACD=\angle CAM = 45^{\circ}$,$\angle MAR=\angle CMT$,
∴$AM = MC$,
∴$\triangle AMR\cong\triangle MCT(AAS)$,
∴$AR = MT = 2 - q = 2 - n$,$MR = CT = n = 3 - q$,
∴$n=\frac{3}{2}$,$q=\frac{3}{2}$,
∴$M(\frac{3}{2},\frac{3}{2})$。
设直线 $CD$ 的解析式为 $y = rx + t$,
则有 $\begin{cases}\frac{3}{2}r + t=\frac{3}{2},\\3r + t = 2,\end{cases}$ 解得 $\begin{cases}r=\frac{1}{3},\\t = 1,\end{cases}$
∴直线 $CD$ 的解析式为 $y=\frac{1}{3}x + 1$。
(3)如图 2,设 $P(p,2p - 4)$。

∵$A(2,0)$,$CM\perp x$ 轴,点 $H$ 在直线 $CM$ 上,
∴点 $H$ 的横坐标为 $3$。
∵四边形 $AHQP$ 为菱形,
∴$Q(p + 1,\frac{1}{3}p+\frac{4}{3})$,$H(3,\frac{16}{3}-\frac{5}{3}p)$,$AP = AH$,
∴$(p - 2)^{2}+(2p - 4)^{2}=(3 - 2)^{2}+(\frac{16}{3}-\frac{5}{3}p)^{2}$,
解得 $p=\frac{1 + 3\sqrt{2}}{2}$ 或 $p=\frac{1 - 3\sqrt{2}}{2}$,
∴点 $P$ 的坐标为 $(\frac{1 + 3\sqrt{2}}{2},3\sqrt{2}-3)$ 或 $(\frac{1 - 3\sqrt{2}}{2},-3\sqrt{2}-3)$。
【解】
(1)
∵直线 $y = 2x + b$ 与 $x$ 轴、$y$ 轴分别交于点 $A$,$B$,
∴$B(0,b)$,$A(-\frac{b}{2},0)$。
∵$S_{\triangle AOB}=\frac{1}{2}OA\cdot OB = 4$,
∴$\frac{1}{2}\times(-\frac{b}{2})\times(-b) = 4$,解得 $b = -4$ 或 $b = 4$ (舍去),
∴$b$ 的值为 $-4$,
∴直线 $AB$ 的解析式为 $y = 2x + b = 2x - 4$。
∵$C(3,m)$ 是直线 $AB$ 上一点,
∴$m = 2\times3 - 4 = 2$。
(2)
∵$b$ 的值为 $-4$,$m$ 的值为 $2$,
∴$B(0,-4)$,$A(2,0)$,$C(3,2)$。
如图 1,过点 $A$ 作 $AM\perp CD$ 于点 $M$,过点 $M$ 作 $MR\perp x$ 轴于点 $R$,过点 $C$ 作 $CT\perp MR$ 于点 $T$,设 $M(q,n)$。

∴$\angle ARM=\angle MTC = 90^{\circ}$,$\angle AMC = 90^{\circ}$。
∵$\angle ACD = 45^{\circ}$,$\angle AMR+\angle MAR=\angle AMR+\angle CMT = 90^{\circ}$,
∴$\angle ACD=\angle CAM = 45^{\circ}$,$\angle MAR=\angle CMT$,
∴$AM = MC$,
∴$\triangle AMR\cong\triangle MCT(AAS)$,
∴$AR = MT = 2 - q = 2 - n$,$MR = CT = n = 3 - q$,
∴$n=\frac{3}{2}$,$q=\frac{3}{2}$,
∴$M(\frac{3}{2},\frac{3}{2})$。
设直线 $CD$ 的解析式为 $y = rx + t$,
则有 $\begin{cases}\frac{3}{2}r + t=\frac{3}{2},\\3r + t = 2,\end{cases}$ 解得 $\begin{cases}r=\frac{1}{3},\\t = 1,\end{cases}$
∴直线 $CD$ 的解析式为 $y=\frac{1}{3}x + 1$。
(3)如图 2,设 $P(p,2p - 4)$。

∵$A(2,0)$,$CM\perp x$ 轴,点 $H$ 在直线 $CM$ 上,
∴点 $H$ 的横坐标为 $3$。
∵四边形 $AHQP$ 为菱形,
∴$Q(p + 1,\frac{1}{3}p+\frac{4}{3})$,$H(3,\frac{16}{3}-\frac{5}{3}p)$,$AP = AH$,
∴$(p - 2)^{2}+(2p - 4)^{2}=(3 - 2)^{2}+(\frac{16}{3}-\frac{5}{3}p)^{2}$,
解得 $p=\frac{1 + 3\sqrt{2}}{2}$ 或 $p=\frac{1 - 3\sqrt{2}}{2}$,
∴点 $P$ 的坐标为 $(\frac{1 + 3\sqrt{2}}{2},3\sqrt{2}-3)$ 或 $(\frac{1 - 3\sqrt{2}}{2},-3\sqrt{2}-3)$。
查看更多完整答案,请扫码查看


