《2025年天府前沿九年级数学上册北师大版》

1. 如图所示几何体的主视图是 ()

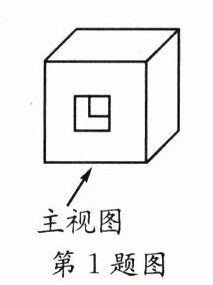
A.
B.
C.
D.

答案： D

2. 一元二次方程$x^{2}-5x+6= 0$的解为 ()
A. $x_{1}= 2,x_{2}= -3$
B. $x_{1}= -2,x_{2}= 3$
C. $x_{1}= -2,x_{2}= -3$
D. $x_{1}= 2,x_{2}= 3$

答案： D

3. 一个不透明的袋子中装有2个红球和若干个黄球,这些球除颜色不同外其他都相同.经过多次试验发现,摸出红球的频率稳定在$\frac {1}{3}$左右,则袋子中的黄球个数最有可能是 ()
A. 1
B. 2
C. 4
D. 6

答案： C

4. 如图,在$△ABC$中,$DE// BC,EF// AB$,要判定四边形DBFE是菱形,还需要添加的条件可以是 ()

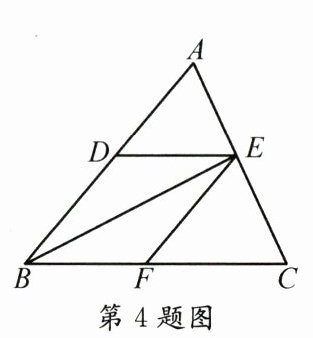
A. $AB= AC$
B. $AD= BD$
C. $BE平分∠ABC$
D. $BE⊥AC$

答案： C

5. 函数$y= kx+b$的图象如图所示,则关于x的一元二次方程$x^{2}+bx+k-1= 0$的根的情况是 ()

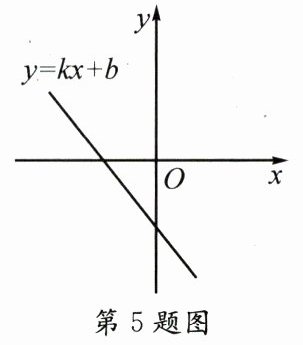
A. 没有实数根
B. 有两个相等的实数根
C. 有两个不相等的实数根
D. 无法确定

答案： C

6. 某种花卉每盆的盈利与每盆的株数有一定的关系,每盆植3株时,平均每株盈利4元;若每盆增加1株,平均每株盈利减少0.5元.要使每盆的盈利达到15元,每盆应多植多少株?设每盆多植x株,则可以列出的方程是 ()
A. $(3+x)(4-0.5x)= 15$
B. $(x+3)(4+0.5x)= 15$
C. $(x+4)(3-0.5x)= 15$
D. $(x+1)(4-0.5x)= 15$

答案： A