《2025年天府前沿九年级数学上册北师大版》

20. 如图,在菱形 $ABCD$ 中,$E$ 是边 $CD$ 的中点,$EF \perp AB$ 交 $AB$ 的延长线于点 $F$,若 $BF:CE = 1:2$,$EF = \sqrt{7}$,则菱形 $ABCD$ 的边长是____.

答案： 4

21. 如图,在矩形 $ABCD$ 中,$BC ＜ AB$.若点 $P$ 满足 $BP \perp AC$,且 $BP = AC$,则 $\angle CDP = $____.

答案： $45^{\circ}$

22. 如图,在平面直角坐标系中,正方形 $ABCD$ 的顶点 $A$ 与原点 $O$ 重合,点 $B$ 在 $x$ 轴的正半轴上,点 $D$ 在 $y$ 轴的正半轴上,在边 $CD$ 的上方作等腰三角形 $CDE$,使 $DC = DE$,连接 $AE$,过点 $D$ 作 $AE$ 的垂线,垂足为 $G$,交 $EC$ 的延长线于点 $F$,连接 $AF$.若点 $D$ 的坐标为 $(0,\sqrt{10})$,$CF$ 的长度为 2,则点 $E$ 的坐标为____.

答案： $(\frac{4\sqrt{10}}{5},\frac{8\sqrt{10}}{5})$

23. 定义:在平面直角坐标系 $xOy$ 中,若矩形 $ABCD$ 的对角线 $AC$ 与 $x$ 轴平行,且对角线 $BD$ 在直线 $y = kx(k ＜ 0)$ 上,则称矩形 $ABCD$ 为“$k$ 率矩形”. 如图,矩形 $ABCD$ 为“$-1$ 率矩形”,点 $A(m,-\frac{m}{2} - 1)$,且直线 $y = -3x - 2$ 平分该矩形的面积,则点 $C$ 的坐标为____.

答案： $(2,1)$

24. (8 分)如图,在矩形 $ABCD$ 中,点 $E$,$F$ 分别在边 $AD$,$BC$ 上,将矩形 $ABCD$ 沿直线 $EF$ 折叠,使点 $B$ 恰好与点 $D$ 重合,点 $A$ 落在点 $A'$ 处,$G$ 为线段 $EF$ 上一动点,过点 $G$ 作 $GM \perp AD$,$GN \perp FD$,垂足分别为 $M$,$N$,以 $GM$,$GN$ 为邻边构造平行四边形 $GMHN$,连接 $DG$,作 $FI \perp AD$ 于点 $I$.若平行四边形 $GMHN$ 的周长为 $4\sqrt{10}$,$AE = 3$,求 $EF$ 的长.

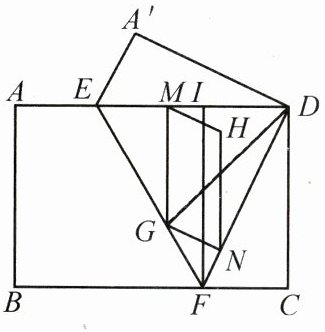
答案： 【解】
∵$FI\perp AD$ 于点 $I$，
∴$\angle DIF=\angle EIF = 90^{\circ}$。
∵四边形 $GMHN$ 是平行四边形，
∴$GM = HN$，$GN = HM$。
∵平行四边形 $GMHN$ 的周长为 $4\sqrt{10}$，
∴$2(GM + GN)=4\sqrt{10}$，
∴$GM + GN = 2\sqrt{10}$。
∵四边形 $ABCD$ 是矩形，
∴$AD// BC$，$\angle A=\angle B=\angle C=\angle ADC = 90^{\circ}$，
∴$\angle DEF=\angle BFE$。
由折叠可知，$\angle DFE=\angle BFE$，$A'E = AE = 3$，$A'D = AB = CD$，
∴$\angle DEF=\angle DFE$，
∴$DE = DF$。
∵$GM\perp AD$ 于点 $M$，$GN\perp FD$ 于点 $N$，
∴$S_{\triangle DEF}=\frac{1}{2}DE\cdot FI=\frac{1}{2}DE\cdot GM+\frac{1}{2}DF\cdot GN$，
∴$FI = GM + GN = 2\sqrt{10}$。
∵$\angle DIF=\angle IDC=\angle C = 90^{\circ}$，
∴四边形 $CDIF$ 是矩形，
∴$CD = FI = 2\sqrt{10}$。
∵$\angle A'=\angle C = 90^{\circ}$，$DE = DF$，$A'D = CD$，
∴$Rt\triangle A'DE\cong Rt\triangle CDF(HL)$，
∴$A'E = CF=ID = 3$，
∴$DE = DF=\sqrt{CD^{2}+CF^{2}}=\sqrt{(2\sqrt{10})^{2}+3^{2}} = 7$，
∴$IE = DE - ID = 7 - 3 = 4$，
∴$EF=\sqrt{FI^{2}+IE^{2}}=\sqrt{(2\sqrt{10})^{2}+4^{2}} = 2\sqrt{14}$。