第43页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
15. (每小题7分,共14分)
(1)已知$y= y_1+y_2$,$y_1与(x-1)$成正比例,$y_2与(x+1)$成反比例,当$x= 0$时,$y= -3$,当$x= 1$时,$y= -1$,求$y$的表达式.
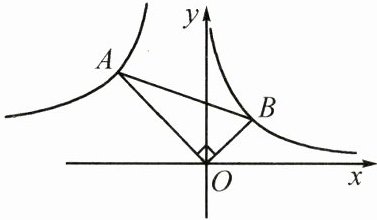
(2)如图,在$Rt\triangle AOB$中,$\angle AOB= 90^{\circ}$,$OA= 4$,$OB= 2$,点$B在反比例函数y= \frac{2}{x}$的图象上,求图中过点$A$的双曲线的解析式.
(1)已知$y= y_1+y_2$,$y_1与(x-1)$成正比例,$y_2与(x+1)$成反比例,当$x= 0$时,$y= -3$,当$x= 1$时,$y= -1$,求$y$的表达式.
(2)如图,在$Rt\triangle AOB$中,$\angle AOB= 90^{\circ}$,$OA= 4$,$OB= 2$,点$B在反比例函数y= \frac{2}{x}$的图象上,求图中过点$A$的双曲线的解析式.

答案:
(1)【解】
∵$y_1$与$(x - 1)$成正比例,$y_2$与$(x + 1)$成反比例,
∴$y_1 = k_1(x - 1)$,$y_2 = \frac{k_2}{x + 1}$。
∵$y = y_1 + y_2$,当$x = 0$时,$y = -3$,当$x = 1$时,$y = -1$,
∴$\begin{cases}-3 = -k_1 + k_2 \\ -1 = \frac{1}{2}k_2\end{cases}$,
∴$k_2 = -2$,$k_1 = 1$,
∴$y = x - 1 - \frac{2}{x + 1}$。
(2)【解】如图,过点$A$作$AC \perp x$轴于点$C$,过点$B$作$BD \perp x$轴于点$D$。
设点$B$的坐标是$(m, n)$,
因为点$B$在函数$y = \frac{2}{x}$的图象上,所以$mn = 2$。
由题设易得$\triangle ACO \sim \triangle ODB$,则$\frac{AC}{OD} = \frac{OC}{BD} = \frac{AO}{BO} = \frac{4}{2} = 2$,
则$BD = n$,$OD = m$,则$AC = 2m$,$OC = 2n$。
设过点$A$的双曲线的解析式是$y = \frac{k}{x}$,点$A$的坐标是$(-2n, 2m)$,
把点$A$的坐标代入,得$2m = \frac{k}{-2n}$,则$k = -4mn = -8$,
所以图中过点$A$的双曲线的解析式是$y = -\frac{8}{x}$。
(1)【解】
∵$y_1$与$(x - 1)$成正比例,$y_2$与$(x + 1)$成反比例,
∴$y_1 = k_1(x - 1)$,$y_2 = \frac{k_2}{x + 1}$。
∵$y = y_1 + y_2$,当$x = 0$时,$y = -3$,当$x = 1$时,$y = -1$,
∴$\begin{cases}-3 = -k_1 + k_2 \\ -1 = \frac{1}{2}k_2\end{cases}$,
∴$k_2 = -2$,$k_1 = 1$,
∴$y = x - 1 - \frac{2}{x + 1}$。
(2)【解】如图,过点$A$作$AC \perp x$轴于点$C$,过点$B$作$BD \perp x$轴于点$D$。
设点$B$的坐标是$(m, n)$,
因为点$B$在函数$y = \frac{2}{x}$的图象上,所以$mn = 2$。
由题设易得$\triangle ACO \sim \triangle ODB$,则$\frac{AC}{OD} = \frac{OC}{BD} = \frac{AO}{BO} = \frac{4}{2} = 2$,
则$BD = n$,$OD = m$,则$AC = 2m$,$OC = 2n$。
设过点$A$的双曲线的解析式是$y = \frac{k}{x}$,点$A$的坐标是$(-2n, 2m)$,
把点$A$的坐标代入,得$2m = \frac{k}{-2n}$,则$k = -4mn = -8$,
所以图中过点$A$的双曲线的解析式是$y = -\frac{8}{x}$。
查看更多完整答案,请扫码查看


