《2025年天府前沿九年级数学上册北师大版》

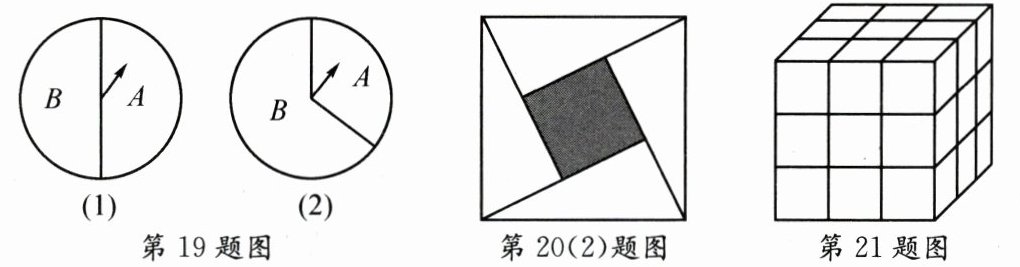
19. 如图,有两个转盘,在每个转盘各自的两个扇形区域中分别标有 $A, B$, 分别转动转盘,当转盘停止时,若事件“指针都落在标有字母 $A$ 的扇形区域内”的概率是 $\frac{1}{6}$, 则转盘(2)中标有字母 $B$ 的扇形的圆心角的度数是 ______.

答案： $240^{\circ}$

20. (1) 从 $-1,0, \frac{1}{4}, 2$ 这 4 个数中任取一个数,作为关于 $x$ 的一元二次方程 $k x^2-x+1= 0$ 的 $k$ 值,则所得的方程中有两个不相等的实数根的概率是 ______.
(2) 如图所示是“赵爽弦图”飞镖板,是由直角边长分别为 2 和 1 的四个直角三角形和一个小正方形(阴影部分)拼成. 某人向该游戏板投掷飞镖一次(假设飞镖落在游戏板上),则飞镖落在阴影部分的概率是 ______.

答案：
(1)$\frac{1}{4}$
(2)$\frac{1}{5}$

21. 如图,将一个棱长为 3 的正方体的表面涂上红色,再把它分割成棱长为 1 的小正方体,从中任取一个小正方体,则取得的小正方体恰有三个面涂有红色的概率为 ______.

答案： $\frac{8}{27}$

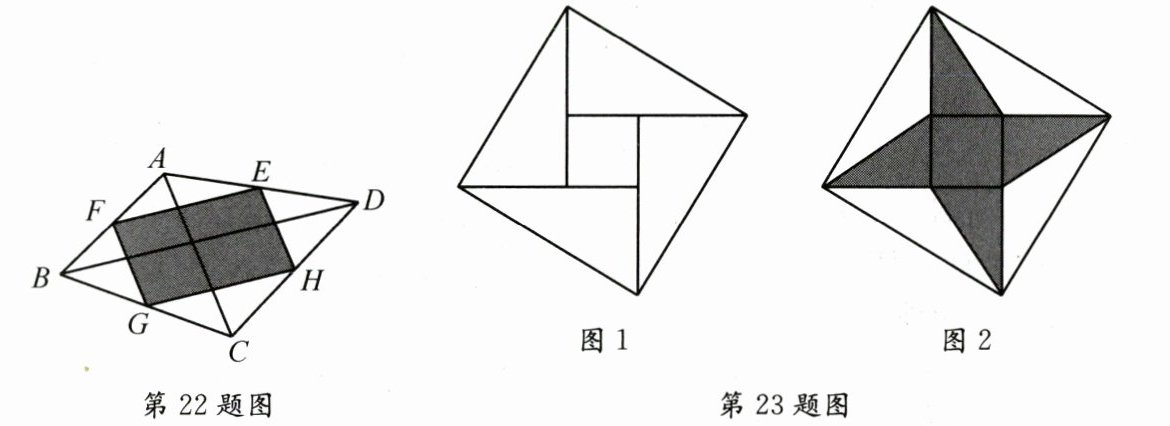
22. 如图,顺次连接四边形 $A B C D$ 各边中点得到四边形 $E F G H$. 将一个飞镖随机投掷到四边形 $A B C D$ 上,则飞镖落在阴影区域(飞镖落在区域分界线时,忽略不计)的概率是 ______.

答案： $\frac{1}{2}$

23. 如图,四个全等的直角三角形围成一个大正方形,中间是个小正方形,这个图形是我国汉代数学家赵爽在注解《周髀算经》时给出的,人们称它为“赵爽弦图”. 现分别连接大、小正方形的四组顶点得到图 2 所示的“风车”图案(阴影部分). 若图 1 中的四个直角三角形的较长直角边为 9,较短直角边为 5,现随机向图 2 大正方形内掷一枚小针,则针尖落在阴影区域的概率为 ______.

答案： $\frac{28}{53}$

24. (8 分) 为保证每位同学在学校组织的课外体育活动中,都能参与自己最喜欢的球类项目,学校体育社团随机抽取部分同学进行“最喜欢的球类项目”的调查(每人只能选择一项),根据调查结果绘制成以下两幅不完整的统计图.

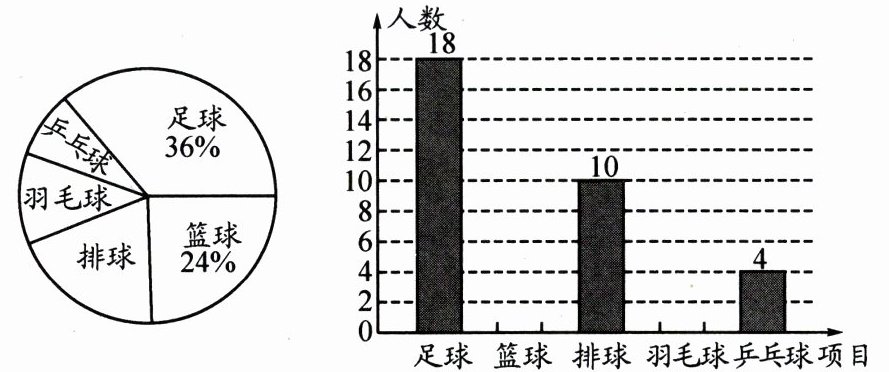
请根据统计图,解答下列问题:
(1) 本次调查的总人数是 ______,估计全校 1500 名学生中最喜欢乒乓球项目的有 ______ 人;
(2) 补全条形统计图;
(3) 学校体育社团为了制订训练计划,将从最喜欢篮球项目的甲、乙、丙、丁四名同学中任选两名进行个别访谈,请用列表或画树状图的方法,求抽取的两人恰好是甲和乙的概率.

答案：
【解】
(1)本次调查的总人数是$18\div36\% = 50$，
估计全校1500名学生中最喜欢乒乓球项目的有$1500\times\frac{4}{50}=120$(人).
故答案为50；120.
(2)根据题意，得最喜欢篮球的有$50\times24\% = 12$(人)，
最喜欢羽毛球的有$50 - 18 - 12 - 10 - 4 = 6$(人).
补全条形统计图如下图所示.

(3)画树状图如下图所示.

由树状图可知，共有12种等可能的结果，其中抽取两人恰好是甲和乙的结果有2种，
$\therefore$抽取的两人恰好是甲和乙的概率为$\frac{2}{12}=\frac{1}{6}$.