《2025年天府前沿九年级数学上册北师大版》

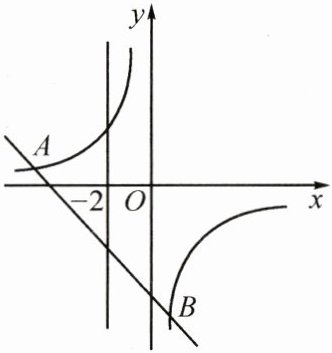
18. (9分)如图,在平面直角坐标系中,一次函数$y= kx+b的图象与反比例函数y= \frac{m}{x}的图象交于A(-6,1)$,$B(1,n)$两点.
(1)求反比例函数和一次函数的解析式;
(2)$P是直线x= -2$上的一个动点,$\triangle PAB$的面积为21,求点$P$的坐标;
(3)点$Q在反比例函数y= \frac{m}{x}$位于第四象限的图象上,$\triangle QAB$的面积为21,请直接写出点$Q$的坐标.

答案： 【解】
(1)把点$A(-6, 1)$代入$y = \frac{m}{x}$，得$1 = \frac{m}{-6}$，
∴$m = -6$，
∴该反比例函数的解析式为$y = -\frac{6}{x}$。
把点$B(1, n)$代入$y = -\frac{6}{x}$，得$n = -6$，
∴$B(1, -6)$。
把点$A(-6, 1)$，$B(1, -6)$代入$y = kx + b$，得$\begin{cases}-6k + b = 1 \\ k + b = -6\end{cases}$，解得$\begin{cases}k = -1 \\ b = -5\end{cases}$，
∴该一次函数的解析式为$y = -x - 5$。
(2)如图1，设直线$x = -2$交直线$AB$于点$H$。
在$y = -x - 5$中，令$x = -2$，得$y = -3$，
∴$H(-2, -3)$。
∵$\triangle PAB$的面积为$21$，
∴$\frac{1}{2}PH \cdot |x_B - x_A| = 21$，
即$\frac{1}{2}PH \times (1 + 6) = 21$，
∴$PH = 6$。
设点$P$的坐标为$(-2, y_P)$。
∴$|y_P + 3| = 6$，解得$y_P = 3$或$y_P = -9$，
∴点$P$的坐标为$(-2, 3)$或$(-2, -9)$。
(3)过点$Q$作$QM // x$轴交直线$AB$于点$M$，如图2所示。
设$Q(t, -\frac{6}{t})$，在$y = -x - 5$中，令$y = -\frac{6}{t}$，得$x = \frac{6}{t} - 5$，
∴$M(\frac{6}{t} - 5, -\frac{6}{t})$，
∴$MQ = |\frac{6}{t} - 5 - t|$。
∵$\triangle QAB$的面积为$21$，
∴$\frac{1}{2}MQ \cdot |y_A - y_B| = 21$，
即$\frac{1}{2} \times |\frac{6}{t} - 5 - t| \times 7 = 21$，
∴$\frac{6}{t} - 5 - t = 6$或$\frac{6}{t} - 5 - t = -6$，
解得$t = \frac{-11 \pm \sqrt{145}}{2}$或$t = -2$或$t = 3$。
经检验，$t = \frac{-11 + \sqrt{145}}{2}$，$t = 3$符合题意。
∴点$Q$的坐标为$(\frac{-11 + \sqrt{145}}{2}, -\frac{11 + \sqrt{145}}{2})$或$(3, -2)$。

19. 如图,矩形$AOCB的两边OC$,$OA分别位于x$轴、$y$轴上,点$B的坐标为(-\frac{20}{3},5)$,$D是AB$边上的一点.将$\triangle ADO沿直线OD$翻折,使点$A恰好落在对角线OB上的点E$处.若点$E$在一反比例函数的图象上,那么该反比例函数的解析式是______.

答案： $y = -\frac{12}{x}$

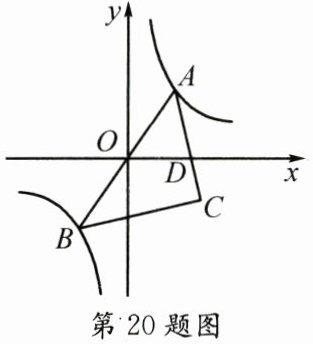
20. 如图,反比例函数$y= \frac{k}{x}的图象经过点(-1,-2\sqrt{2})$,$A$是该图象第一象限分支上的动点,连接$AO并延长交另一分支于点B$,以$AB为斜边作等腰直角三角形ABC$,顶点$C$在第四象限,$AC与x轴交于点D$.当$\frac{AD}{CD}= \sqrt{2}$时,点$C$的坐标为______.

答案： $(2, -\sqrt{2})$

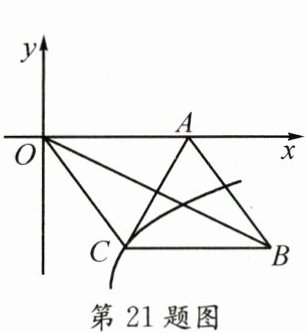
21. 如图,在平面直角坐标系中,点$A的坐标是(5,0)$,函数$y= \frac{k}{x}(x\gt0)的图象经过菱形OABC的顶点C$.若$OB\cdot AC= 40$,则$k$的值为______.

答案： -12