《2025年天府前沿九年级数学上册北师大版》

7. 下列说法正确的是 ()
A. 顺次连接对角线互相垂直的四边形各边中点所得的四边形一定是菱形
B. 反比例函数$y= -\frac {3}{x}$的图象是y随x的增大而增大
C. 以原点O为位似中心,将$△ABC$放大到原来的两倍,若点A的坐标为$(2,3)$,则点A的对应点$A'的坐标为(4,6)$
D. 点C是线段AB的黄金分割点,且$AC＞BC,AB= 200$,则AC的长度为$100(\sqrt {5}-1)$

答案： D

8. 如图,在直角坐标系xOy中,$A(-4,0),B(0,2)$,连接AB并延长到点C,连接CO,若$△COB\backsim △CAO$,则点C的坐标为 ()

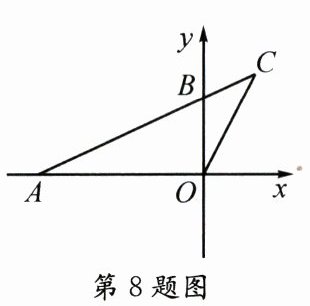
A. $(1,\frac {5}{2})$
B. $(\frac {4}{3},\frac {8}{3})$
C. $(\sqrt {5},2\sqrt {5})$
D. $(\sqrt {3},2\sqrt {3})$

答案： B

9. 若$\frac {x}{3}= \frac {y}{4}= \frac {z}{6}≠0$,则$\frac {x-z}{y}$的值为______.

答案： $-\frac{3}{4}$

10. 有四张大小和背面完全相同的不透明卡片,正面分别印有等边三角形、平行四边形、菱形和圆,将这四张卡片背面朝上洗匀,从中随机抽取两张卡片,所抽取的卡片正面上的图形既是轴对称图形,又是中心对称图形的概率是______.

答案： $\frac{1}{6}$

11. 一元二次方程$kx^{2}-2x-2= 0$有实数根,则k的取值范围是______.

答案： $k \geq -\frac{1}{2}$且$k \neq 0$

12. 如图,$△ABC\backsim △CBD,AB= 4,BD= 6$,则$BC= $______.

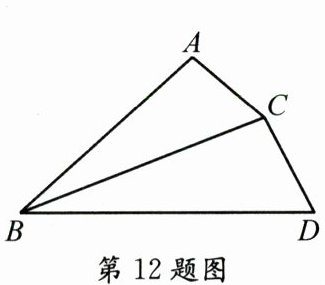
答案： $2\sqrt{6}$

13. 如图,在正方形ABCD中,对角线AC,BD相交于点O,E是OB的中点,连接AE并延长交BC于点F.若$△BEF$的面积为1,则正方形ABCD的面积为______.

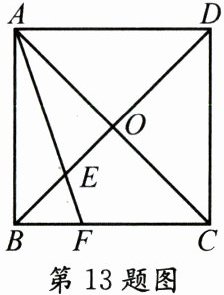
答案： 24

14. (每小题5分,共10分)用适当的方法解方程:
(1)$2x^{2}-6x+1= 0;$
(2)$x^{2}-2x-8= 0.$

答案：
(1)【解】$\because a = 2$，$b = -6$，$c = 1$，$\therefore \Delta = b^{2} - 4ac = 6^{2} - 4 \times 2 \times 1 = 28$，
则$x = \frac{-b \pm \sqrt{b^{2} - 4ac}}{2a} = \frac{6 \pm 2\sqrt{7}}{4} = \frac{3 \pm \sqrt{7}}{2}$，$\therefore x_{1} = \frac{3 + \sqrt{7}}{2}$，$x_{2} = \frac{3 - \sqrt{7}}{2}$。
(2)【解】$\because x^{2} - 2x - 8 = 0$，$\therefore (x + 2)(x - 4) = 0$，
$\therefore x + 2 = 0$或$x - 4 = 0$，则$x_{1} = -2$，$x_{2} = 4$。