《2025年天府前沿九年级数学上册北师大版》

7. 如图,已知 $ \triangle ABC $ 和 $ \triangle DEF $ 是以点 $ O $ 为位似中心的位似图形, $ OA:AD = 2:3 $, $ \triangle ABC $ 的面积为 4,则 $ \triangle DEF $ 的面积为 ()

A. $ 6 $
B. $ 10 $
C. $ 25 $
D. $ 12 $

答案： C

8. 如图, $ EB $ 为驾驶员的盲区,驾驶员的眼睛点 $ P $ 处与地面 $ BE $ 的距离为 $ 1.6 $ 米,车头 $ FACD $ 近似看成一个矩形,且满足 $ 3FD = 2FA $. 若盲区 $ EB $ 的长度是 $ 6 $ 米,则车宽 $ FA $ 的长度为 ()

A. $ \frac{11}{7} $ 米
B. $ \frac{12}{7} $ 米
C. $ \frac{13}{7} $ 米
D. $ 2 $ 米

答案： B

9. 在比例尺为 $ 1:50000 $ 的地图上量出 $ A $, $ B $ 两地的距离是 $ 12 \text{ cm} $,那么 $ A $, $ B $ 两地的实际距离是 ______ 千米.

答案： 6

10. 如图,直线 $ l_1 // l_2 // l_3 $,直线 $ AC $ 和 $ DF $ 被 $ l_1 $, $ l_2 $, $ l_3 $ 所截, $ AB = 5 $, $ BC = 6 $, $ EF = 4 $,则 $ DE $ 的长为 ______.

答案： $\frac{10}{3}$

11. 如果两个相似三角形的周长的比为 $ 1:4 $,那么周长较小的三角形与周长较大的三角形对应角平分线的比为 ______.

答案： $1:4$

12. 如图是洞孔成像原理的示意图,物体 $ AB // $ 物像 $ CD $,根据图中标注的尺寸,如果物体 $ AB $ 长 $ 8 \text{ cm} $,那么物像 $ CD $ 的长是 ______.

答案： $\frac{16}{5}cm$

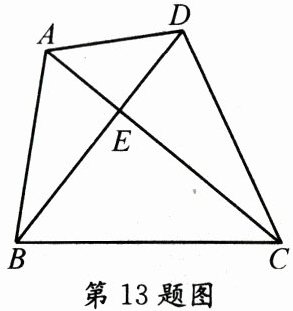
13. 如图,在四边形 $ ABCD $ 中,对角线 $ AC $ 与 $ BD $ 相交于点 $ E $,且 $ \angle CAB = \angle CBD $. 若 $ AB = 4 $, $ AC = 6 $, $ BC = 5 $, $ BD = \frac{16}{3} $,则 $ DE $ 的长为 ____.

答案： 2

14. (每小题 7 分,共 14 分)
(1) 如图,延长正方形 $ ABCD $ 的一边 $ CB $ 至点 $ E $, $ ED $ 与 $ AB $ 相交于点 $ F $,过点 $ F $ 作 $ FG // BE $ 交 $ AE $ 于点 $ G $,求证: $ GF = FB $.

(2) 如图, $ AB \cdot AE = AD \cdot AC $,且 $ \angle 1 = \angle 2 $,求证: $ \triangle ABC \sim \triangle ADE $.

答案：
(1)【证明】
∵四边形$ABCD$为正方形，
∴$BF// CD$，
∴$\frac{BF}{CD}=\frac{EF}{ED}$。
∵$FG// BE$，
∴$GF// AD$，
∴$\frac{GF}{AD}=\frac{EF}{ED}$，
∴$\frac{GF}{AD}=\frac{BF}{CD}$。
又$AD = CD$，
∴$GF = BF$。
(2)【证明】
∵$AB\cdot AE = AD\cdot AC$，
∴$\frac{AB}{AD}=\frac{AC}{AE}$。
又
∵$∠1 = ∠2$，
∴$∠2 + ∠BAE = ∠1 + ∠BAE$，即$∠BAC = ∠DAE$，
∴$△ABC\backsim △ADE$。