《2024年孟建平单元测试九年级数学全一册浙教版》

15. 2023年5月28日,C919商业首航完成——中国民航商业运营国产大飞机正式起步.12时31分航班抵达北京首都机场,穿过隆重的“水门礼”(寓意“接风洗尘”,是国际民航中高级别的礼仪). 如图1,在一次“水门礼”的预演中,两辆消防车面向飞机喷射水柱,喷射的两条水柱近似看作形状相同的抛物线的一部分. 如图2,当两辆消防车喷水口 $A,B$的水平距离为80米时,两条水柱在抛物线的顶点 $H$处相遇. 此时相遇点 $H$距地面20米,喷水口 $A,B$距地面均为4米. 若两辆消防车同时后退10米,两条水柱的形状及喷水口 $A',B'$到地面的距离均保持不变,则此时两条水柱相遇点 $H'$距地面______米.

答案： 19

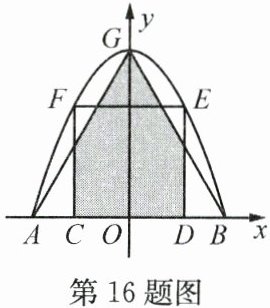
16. 如图,抛物线与 $x$轴交于点 $A,B$,与 $y$轴交于点 $G$,正方形 $CDEF$的边 $CD$在 $x$轴上,点 $E,F$在抛物线上,连结 $GA,GB$. 若$\triangle ABG$是正三角形,$AB = 2$,则阴影部分的面积为______.

答案： 2−$\frac{\sqrt{3}}{3}$

17. (6分)已知函数 $y = x^{2}+mx + m - 3$.
(1) 求证:不论 $m$为何实数,此二次函数的图象与 $x$轴都有两个不同交点;
(2) 若函数有最小值 -2,求函数表达式.

答案： 证明:
(1)令y=x²+mx+m−3=0,
∵b²−4ac=m²−4(m−3)=m²−4m+12=(m−2)²+8＞0,
∴不论m为何实数，此二次函数的图象与r轴都有两个不同交点.　　
(2)解:由题意，得$\frac{4ac−b²}{4a}$=$\frac{4(m−3)−m²}{4}$=−2,
整理,得m²−4m+4=0,
解得m1=m2=2,
∴所求函数表达式为y=x²+2x−1.

18. (6分)已知抛物线 $y = ax^{2}+bx - 5$经过点 $M(-1,1)$,$N(2,-5)$.
(1) 求 $a,b$的值;
(2) 若 $P(4,y_{1})$,$Q(m,y_{2})$是抛物线上不同的两点,且 $y_{2}=22 - y_{1}$,求 $m$的值.

答案： 解:
(1)
∵抛物线y=ax²+bx−5经过点M(−1,1),N(2,−5),
∴$\begin{cases}{a-b-5=1 } \\ {4a+b-5=-5} \end{cases}$
解得$a=2,b=-4$
(2)由
(1)知,抛物线的解析式为y=2x²−4x−5,
$∴当x=4时,y_1=2×4²−4×4−5=11,$
$∴y_2=22−y_1=11,$
∴(4,11)与(m,11)关于对称轴对称,
∴$\frac{4+m}{2}=\frac{−4}{2×2}$,
解得m=−2.