第53页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
22. (10分)定义:对角线互相垂直的圆内接四边形叫做圆的奇妙四边形.
(1) 如图1,已知四边形ABCD是⊙O的奇妙四边形.若AC=6,BD=8,则S四边形ABCD=______;
(2) 如图2,已知四边形ABCD内接于⊙O,对角线交于点E.若$\overset{\frown}{AD}+\overset{\frown}{BC}\stackrel{m}{=}180°$.
①求证:四边形ABCD是⊙O的奇妙四边形;
②作OM⊥BC于点M.请猜想AD与OM之间的数量关系,并说明理由.
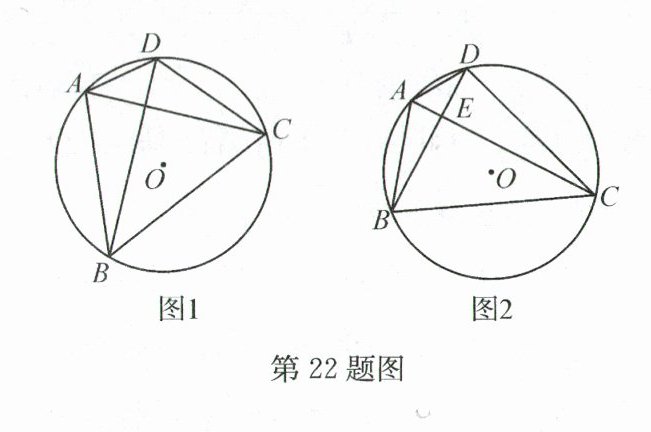
(1) 如图1,已知四边形ABCD是⊙O的奇妙四边形.若AC=6,BD=8,则S四边形ABCD=______;
(2) 如图2,已知四边形ABCD内接于⊙O,对角线交于点E.若$\overset{\frown}{AD}+\overset{\frown}{BC}\stackrel{m}{=}180°$.
①求证:四边形ABCD是⊙O的奇妙四边形;
②作OM⊥BC于点M.请猜想AD与OM之间的数量关系,并说明理由.

答案:
(1)24 解析:记AC与BD的交点为E.
∵四边形ABCD为OO的奇妙四边形,
∴AC⊥BD,
∴S四边形ABCD=S△ACD十SABC=$\frac{1}{2}$AC.DE+$\frac{1}{2}$AC.BE=$\frac{1}{2}$AC(DE+BE)=$\frac{1}{2}$AC.BD=$\frac{1}{2}$×6×8 =24.
(2)①证明:连结OA,OB,OC,OD.
∵AD+BC=180°,
∴∠AOD+∠BOC=180°.
∵∠ACD =$\frac{1}{2}$∠AOD,∠BDC=$\frac{1}{2}$∠BOC,
∴∠ACD+∠BDC=$\frac{1}{2}$(∠AOD+∠BOC)=90°,
∴∠DEC=90°,即AC⊥BD,
∴四边形ABCD是OO的奇妙四边形. ②解:AD=2OM. 理由如下:过点O作ON⊥AD于点N,则AD=2AN,∠AON=$\frac{1}{2}$∠AOD.
∵OVI⊥BC,
∴∠BOM=$\frac{1}{2}$∠BOC.由①得∠A0D+∠B汇C=180°,,
∴∠AON+∠BOM=$\frac{1}{2}$(∠AOD+∠BOC)=90°.
∵∠OBM+∠BOM=90°,
∴∠AON=∠OBM.
∵∠ANO=∠OMB=90°,OA=OB,
∴△AON≌△OBM,
∴AN=OM,
∴AD=2OM.
(1)24 解析:记AC与BD的交点为E.
∵四边形ABCD为OO的奇妙四边形,
∴AC⊥BD,
∴S四边形ABCD=S△ACD十SABC=$\frac{1}{2}$AC.DE+$\frac{1}{2}$AC.BE=$\frac{1}{2}$AC(DE+BE)=$\frac{1}{2}$AC.BD=$\frac{1}{2}$×6×8 =24.
(2)①证明:连结OA,OB,OC,OD.
∵AD+BC=180°,
∴∠AOD+∠BOC=180°.
∵∠ACD =$\frac{1}{2}$∠AOD,∠BDC=$\frac{1}{2}$∠BOC,
∴∠ACD+∠BDC=$\frac{1}{2}$(∠AOD+∠BOC)=90°,
∴∠DEC=90°,即AC⊥BD,
∴四边形ABCD是OO的奇妙四边形. ②解:AD=2OM. 理由如下:过点O作ON⊥AD于点N,则AD=2AN,∠AON=$\frac{1}{2}$∠AOD.
∵OVI⊥BC,
∴∠BOM=$\frac{1}{2}$∠BOC.由①得∠A0D+∠B汇C=180°,,
∴∠AON+∠BOM=$\frac{1}{2}$(∠AOD+∠BOC)=90°.
∵∠OBM+∠BOM=90°,
∴∠AON=∠OBM.
∵∠ANO=∠OMB=90°,OA=OB,
∴△AON≌△OBM,
∴AN=OM,
∴AD=2OM.
23. (12分)小明在学习了《圆周角定理及其推论》后,有这样的学习体会:如图1,在Rt△ABC中,∠C=90°,当AB长度不变时,点C在以AB为直径的圆上运动(不与点A,B重合).
[探索发现]
小明继续探究,在Rt△ABC中,∠C=90°,AB长度不变.如图2,作∠A与∠B的角平分线交于点F,小明计算后发现∠AFB的度数为定值,小明猜想点F也在一个圆上运动.请你计算∠AFB的度数,并简要说明小明猜想的圆的特征;
[拓展应用]
在[探索发现]的条件下,若AB=2√3,求△AFB面积的最大值.
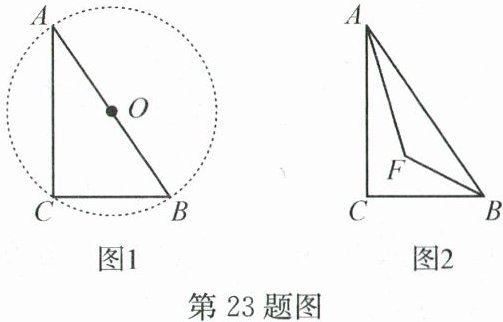
[探索发现]
小明继续探究,在Rt△ABC中,∠C=90°,AB长度不变.如图2,作∠A与∠B的角平分线交于点F,小明计算后发现∠AFB的度数为定值,小明猜想点F也在一个圆上运动.请你计算∠AFB的度数,并简要说明小明猜想的圆的特征;
[拓展应用]
在[探索发现]的条件下,若AB=2√3,求△AFB面积的最大值.

答案:
解:[探索发现]
∵∠ACB=90°,
∴∠CAB+∠CBA =90°.
∵AF是∠CAB的平分线,BF是∠CBA的平分线,
∴∠FAB+∠FBA=45°,
∴∠AFB=135°,
∴点F在以AB为定弦,∠AFB为定角的圆上运动, [拓展应用]如图1,过点F作FH⊥AB 于点H,记AB的中点为D,以AB为底,向外作等腰直角三角形OAB,以OA为半径作⊙O.
∵∠AOB =90°,∠AFB=135°,
∴∠AFB+$\frac{1}{2}$∠AOB=180°,
∴点F在oO上.
∵∠ACB+∠AOB=180°,
∴点O与点C共圆,当点H与点D重合时,FH的长度最大,此时△AFB的面积最大.
∵FH⊥AB,D 是AB的中点,
∴FA=FB,
∴∠FAB=∠FBA=22.5°,
∴∠CAB=∠CBA=45°,
∴△ABC是等腰直角三角形.如图2,连结CF,则C,F,D=点共线,过点F作FP⊥AC于点P,则FP=FD,又
∵∠APF=∠ADF=90°,AF=AF,
∴R;△APF≌Rt△ADF,
∴AP=AD.
∵AB=2$\sqrt{3}$
∴AP=AD=CD=$\frac{1}{2}$AB=√3,
∴AC= $\sqrt{AD+CD°}$=$\sqrt{6}$.
∵∠FPC=90°,∠PCF=$\frac{1}{2}$∠ACB=45°,
∴∠CFP=45°=∠PCF,
∴CP=FP=FD.
∵CP=AC−AP=$\sqrt{6}$ $\sqrt{3}$,
∴FD= $\sqrt{6}$−$\sqrt{3}$,
∴SAF;=$\frac{1}{2}$AB.FD =3√2−3,
∴△AFB面积的最大值为3$\sqrt{2}$−3.
∵∠ACB=90°,
∴∠CAB+∠CBA =90°.
∵AF是∠CAB的平分线,BF是∠CBA的平分线,
∴∠FAB+∠FBA=45°,
∴∠AFB=135°,
∴点F在以AB为定弦,∠AFB为定角的圆上运动, [拓展应用]如图1,过点F作FH⊥AB 于点H,记AB的中点为D,以AB为底,向外作等腰直角三角形OAB,以OA为半径作⊙O.
∵∠AOB =90°,∠AFB=135°,
∴∠AFB+$\frac{1}{2}$∠AOB=180°,
∴点F在oO上.
∵∠ACB+∠AOB=180°,
∴点O与点C共圆,当点H与点D重合时,FH的长度最大,此时△AFB的面积最大.
∵FH⊥AB,D 是AB的中点,
∴FA=FB,
∴∠FAB=∠FBA=22.5°,
∴∠CAB=∠CBA=45°,
∴△ABC是等腰直角三角形.如图2,连结CF,则C,F,D=点共线,过点F作FP⊥AC于点P,则FP=FD,又
∵∠APF=∠ADF=90°,AF=AF,
∴R;△APF≌Rt△ADF,
∴AP=AD.
∵AB=2$\sqrt{3}$
∴AP=AD=CD=$\frac{1}{2}$AB=√3,
∴AC= $\sqrt{AD+CD°}$=$\sqrt{6}$.
∵∠FPC=90°,∠PCF=$\frac{1}{2}$∠ACB=45°,
∴∠CFP=45°=∠PCF,
∴CP=FP=FD.
∵CP=AC−AP=$\sqrt{6}$ $\sqrt{3}$,
∴FD= $\sqrt{6}$−$\sqrt{3}$,
∴SAF;=$\frac{1}{2}$AB.FD =3√2−3,
∴△AFB面积的最大值为3$\sqrt{2}$−3.
查看更多完整答案,请扫码查看


