《2024年孟建平单元测试九年级数学全一册浙教版》

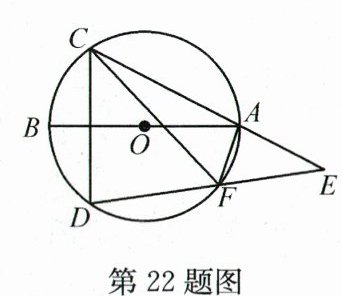
22. (10分)如图,AB是⊙O的直径,弦CD⊥AB,E是CA延长线上的一点,连结DE交⊙O于点F,连结AF,CF.
(1) 若$\overset{\frown}{BD}$的度数是40°,求∠AFC的度数;
(2) 求证:FA平分∠CFE;
(3) 若AB=5,CD=4,CF经过圆心,求CE的长.

答案： 记AB交CD于点H.
(1)解:连结OD,AD.
∵BD的度数是40°,即∠D)B=40°,
∴∠DAB $\frac{1}{2}$∠DOB=20°,
∵AB⊥CD,
∴∠AHD=90°,
∴∠ADH=90°−∠DAB=70°,
∴∠AFC=∠ADH =70°.
(2)证明:
∵AB是直径，AB⊥CD,
∴A)C=A)D,
∴∠ADC=∠ACD,
∵∠ACD+∠AFD=180°,∠AFD+∠AFE=180°,
∴∠ACD=∠AFE,
∵∠AFC=∠ADC,
∴∠AFC=∠AFE,即FA 平分∠CFE.
(3)解:
∵AB是直径,AB⊥CD,
∴CH=$\frac{1}{2}$CD=2,又
∵OC=$\frac{5}{2}$'∠OHC=90°,
∴OH= $\sqrt{OC−CH²}$=$\frac{3}{2}$,...AH=OH+OA=OH+$\frac{1}{2}$AB=4,
∴AC=√CH²+AH=2$\sqrt{5}$
∵CF是直径,
∴∠CAF=90°,即AF⊥CE.由
(2)得FA平分∠CFE,
∴易得AC=AE,
∴CE=2AC =4$\sqrt{5}$

23. (12分)如图1,C,D是半圆ACB上的两点,若直径AB上存在一点P,满足∠APC=∠BPD,则称∠CPD是$\overset{\frown}{CD}$的“幸运角”.
(1) 如图2,AB是⊙O的直径,弦CE⊥AB,D是$\overset{\frown}{BC}$上的一点,连结DE交AB于点P,连结CP.
①∠CPD是$\overset{\frown}{CD}$的“幸运角”吗? 请说明理由;
②设$\overset{\frown}{CD}$的度数为n,请用含n的式子表示$\overset{\frown}{CD}$的“幸运角”度数;
(2) 如图3,在(1)的条件下,若直径AB=10,$\overset{\frown}{CD}$的“幸运角”为90°,DE=8,求CE的长.

答案： 解:
(1)①∠CPD是CD的“幸运角” 理由如下:记CE交AB于点F.
∵AB是⊙O的直径,CE⊥AB,
∴CF=EF,
∴CP=EP,
∴∠CPA=∠EPA,
∵∠DPB ∠EPA,
∴∠DPB=∠CPA,
∴∠CPD是CD的“幸运角”. ②
∵CD的度数为n,
∴∠CED=$\frac{n}{2}$
∵CP=EP,
∴∠ECP=∠CED=$\frac{n}{2}$
∴∠CPD=∠CED+∠ECP=n,
∴CD的“幸运角”度数为n.
(2)如图,连结CO,DO.
∵CD的“幸运角”为90°,即∠CPD=90°,
∴∠COD=90°.
∵AB=10,
∴OC=OD=$\frac{1}{2}$AB=5,
∴CD= $\sqrt{OC+OD}$=5$\sqrt{2}$设CP=EP=x,则PD=8−x,
∴在Rt△CPD中,CP²+PD²=CD²,即x²+(8−x)²=50,解得x1=1,x2=7,即CP=EP=1或7.
∵∠CPD=90°,
∴∠CPE=90°,
∴CE = $\sqrt{CP+EP}$=$\sqrt{2}$或7$\sqrt{2}$.