《2024年孟建平单元测试九年级数学全一册浙教版》

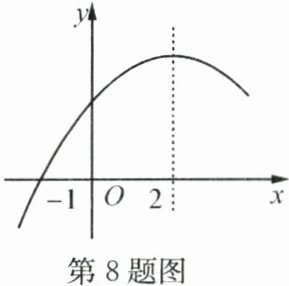
8. 二次函数$y = ax^{2}+bx + c(a\neq0)$的部分图象如图，图象过点$(-1,0)$，对称轴为直线$x = 2$，下列结论：①$4a + b = 0$；②$9a + c＞3b$；③当$x＞-1$时，$y$随$x$的增大而增大；④当函数值$y＜0$时，自变量$x$的取值范围是$x＜-1$或$x＞5$. 其中正确的结论有( )

A. 1个
B. 2个
C. 3个
D. 4个

答案： B解析:
∵对称轴为直线x=2,
∴　$\frac{6}{2a}$=2,
∴b=−4a,
∴4a+b=0,①正确;
∵图象过(−1,0),
∴当x=−3时,y＜0,即9a−3b+c＜0,
∴9a十c＜3b,②错误;由图象可知，当x＜2时,y随x的增大而增大，③错误;由对称性可得，二次函数图象过(5,0),
∴当y＜0时,x＜−1或x＞5,④正确,

9. 如图，在正方形$ABCD$中，点$A$，$C$的坐标分别是$(-1,5)$，$(2,0)$，点$D$在抛物线$y=\frac{1}{3}x^{2}+kx$上，则$k$的值是( )

A. $\frac{1}{3}$
B. $\frac{2}{3}$
C. $\frac{4}{3}$
D. $\frac{7}{3}$

答案： A

10. 定义：在平面直角坐标系中，若点$A$满足横、纵坐标都为整数，则把点$A$叫做“整点”，如：$B(3,0)$，$C(-1,3)$都是“整点”. 抛物线$y = ax^{2}-2ax + a + 2(a＜0)$与$x$轴交于$M$，$N$两点，若该抛物线在点$M$，$N$之间的部分与线段$MN$所围的区域(包括边界)恰有5个整点，则$a$的取值范围是( )
A. $-1\leqslant a＜0$
B. $-2\leqslant a＜-1$
C. $-1\leqslant a＜-\frac{1}{2}$
D. $-2\leqslant a＜0$

答案： B

11. 将抛物线$y = -2(x + 2)^{2}$向右平移3个单位长度，再向下平移4个单位长度得到的抛物线的函数解析式为__________.

答案： y=−2(x−1)²−4

12. 一个不透明的袋中装有红、黄、白三种颜色的球共100个，它们除颜色外都相同，其中黄球个数比白球个数的2倍少5个. 已知从袋中摸出一个球是红球的概率是$\frac{3}{10}$，则从袋中摸出一个球是白球的概率是_______.

答案： $\frac{1}{4}$

13. 某学校组织学生到社区开展公益宣传活动，成立了“垃圾分类”“文明出行”“低碳环保”三个宣传队. 如果小华和小丽每人随机选择参加其中一个宣传队，则两人都到“垃圾分类”宣传队的概率是_______.

答案： $\frac{1}{9}$

14. 有一个开口向下的二次函数，下表是函数中四对$x$与$y$的对应值.

若其中有一对对应值有误，则对于该二次函数，当$y＜-1$时，$x$的取值范围是_______.

答案： x＜0或x＞3解析:
∵抛物线开口向下，
∴抛物线必为先递增再递减，
∴x=−1时y的对应值有误;
∵当x=1和2时,y的值相等,
∴抛物线的对称轴为直线x=$\frac{3}{2}$
∴当x=3和0时,y的值相等，为−1,
∴当y＜−1时,x＜0或x＞3,

15. 二次函数$y = -(x - b)^{2}+4b + 1$与一次函数$y = -x + 5(-1\leqslant x\leqslant5)$的图象只有一个交点，则$b$的取值范围是________.

答案： $2＜b≤12或b=\frac{3}{4}$

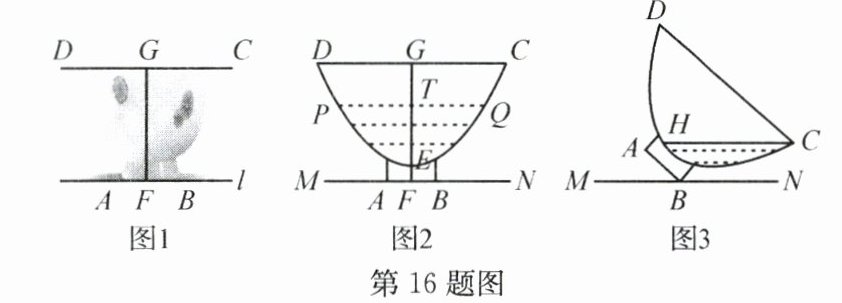
16. 如图1是一个瓷碗，如图2是其截面图，碗体$DEC$呈抛物线状(碗体厚度不计)，碗口宽$CD = 12$cm，此时面汤最大深度$EG = 8$cm.
(1)当面汤的深度$ET$为4 cm时，面汤的直径$PQ$长为_______cm；
(2)如图3，把瓷碗绕点$B$缓缓倾斜倒出部分面汤，当$\angle ABM = 45^{\circ}$时停止，此时碗中液面宽度$CH =$_______cm.

答案：
(1)6$\sqrt{2}$　
(2)$\frac{15}{2}\sqrt{2}$