《2024年孟建平单元测试九年级数学全一册浙教版》

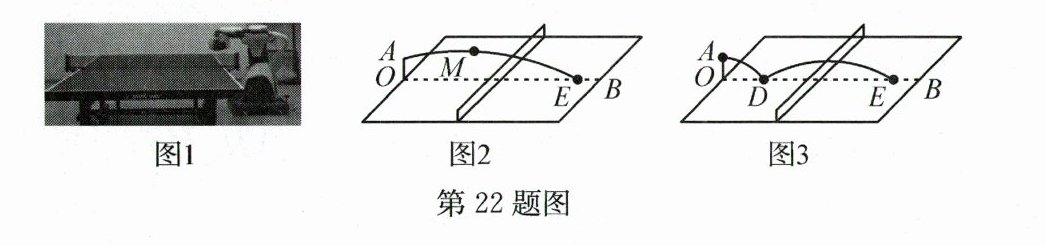
22. (10分)图1是一张带智能发球机的乒乓球桌，它可以自定义设置球的落点、速度、弧度及旋转方式，能更真实地模拟实战。图2是发球机从中线$OB$的端点$O$的正上方0.3 m处的$A$点发球，球呈抛物线在$OB$正上方飞行，当飞行的水平距离为1 m时，达到最高点$M$，其高度为0.4 m。以$O$为原点，$OB,OA$所在直线分别为$x$轴，$y$轴建立平面直角坐标系。
(1) 求图2中抛物线的表达式；
(2) 记图2中的落球点为点$E$，则$OE$的长为多少？
(3) 图3是为了更好地模拟与人对打，将出球方向改变，调整成两跳球的方式，即球从点$A$落到点$D$，再反弹过网落下，反弹后球呈抛物线飞行，且形状与图2中的抛物线形状保持不变，但反弹后的最高高度变为0.2 m。若最后球也落在点$E$，则$OD$的长为多少？

答案： 解:
(1)由题意，得点A,M的坐标分别为(0,0.3),(1,0.4).设抛物线的表达式为y=a(x−1)²十0.4,将点A的坐标代入,得0.3=a((0−1)²+0.4,解得a=−0.1,
∴抛物线的表达式为y=−0.1(x −1)²+0.4.　　
(2)令y=−0.1(x−1)²+0.4=0,解得x=−1(舍去)或x=3,
∴OE=3m.　　
(3)设点D(m,0),由
(2)得点E(3,0)),
∴设抛物线的表达式为y=−0.1(x−m)(x−3)=−0.1.x²+(0.3 +0.1m)x−0.3m,则$\frac{4ac−b²}{4a}$=4×(−0.1)×(4−×0(.−3m0.)1−)(0.3+0.1m)²=0.2,解得m=3+2$\sqrt{2}$(舍去),m2=3−2$\sqrt{2}$
∴OD的长为(3−2$\sqrt{2}$)m.　　点评:本题考查的是二次函数的实际应用问题，解第
(1)问的关键是理解题意，准确得到点A,M的坐标,并利用待定系数法求解即可，解第
(2)问的关键是理解落球点即抛物线与x轴的交点，注意结合实际情况进行取舍，解第
(3)问的关键是理解抛物线形状保持不变即对应二次函数的二次项系数不变.