《2024年孟建平单元测试九年级数学全一册浙教版》

23. (12分)学校门口经常有小贩搞摸奖活动,某小贩在一个黑色的口袋里装有不同颜色的50个小球,其中红球1个,黄球2个,绿球10个,其余为白球,搅拌均匀后,每2元摸1球,奖品的情况标注在球上(如图):
(1) 如果花2元摸1个球,那么摸不到奖的概率是多少?
(2) 如果花4元同时摸2个球,那么获得10元奖品的概率是多少?

答案： 解：
(1)根据题意可得：共50只球，白球的个数为50 - 1 - 2 - 10 = 37，
∴摸不到奖的概率是$\frac{37}{50}$。
(2)获得10元奖品只有一种可能即同时摸出两个黄球. 通过画树状图易知共有50×49 = 2450(种)等可能的情况，其中两次都摸出黄球的情况有2种，
∴获得10元奖品的概率是$\frac{2}{2450}=\frac{1}{1225}$。

24. (12分)某电视台一档综艺节目中,要求嘉宾参加知识竞答,竞答题共10道. 每一题有三个选项,且只有一个选项正确,规定每题答对得2分,答错扣1分,不答得0分,若10道题全部答对则另外再奖励2分. 某位嘉宾已经答对了8道题,剩下2道题他都不确定哪个选项正确.
(1) 若这位嘉宾随机选择一个选项,求他剩下的2道题一对一错的概率;
(2) 这位嘉宾对剩下2题可以都不答,或只随机答1题,或随机答2题,请你从统计与概率的角度分析,采用哪种做法解答剩下2道题更合算.

答案：
解：
(1)因为每小题有三个选项，且只有一个选项是正确的，所以有两个选项是错误的，不妨用“对，错，错”来表示，列表如下：

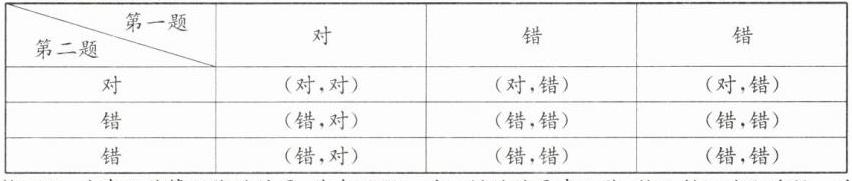
由表格可知，共有9种等可能的结果，其中两题一对错的结果有4种，所以剩下的2道题一对错的概率为$\frac{4}{9}$。
(2)①当2题都不答时，总得分为0 + 2×8 = 16(分)；②当一题不答，一题随机答时，$\because P_{(对)}=\frac{1}{3}$，$P_{(错)}=\frac{2}{3}$，
∴预期总得分为$2\times\frac{1}{3}-1\times\frac{2}{3}+0 + 2×8 = 16$(分)；③当随机答2题时，有两题都对，一对错，两题都错三种可能，所得的分数分别为6分，1分， - 2分，相应的概率分别为$P$(答对2题)$=\frac{1}{9}$，$P$(答对1题)$=\frac{4}{9}$，$P$(两题都答错)$=\frac{4}{9}$，
∴预期总得分为$6\times\frac{1}{9}+1\times\frac{4}{9}-2\times\frac{4}{9}+2×8 = 16\frac{2}{9}$。
∴小明采用随机答2题的方式更合算。