《2024年孟建平单元测试九年级数学全一册浙教版》

21. (10分)如图,已知四边形$ABCD$两条对角线相交于点$E$,$AB = AC = AD$,$AE = 3$,$CE = 1$.
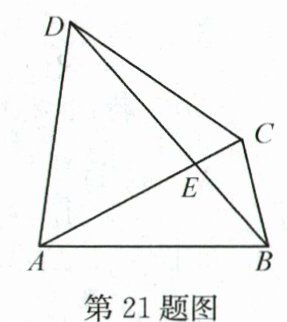
(1) 请用直尺与圆规作$\triangle BCD$的外接圆,并保留作图痕迹;
(2) 求$BE\cdot DE$的值.

答案： 解:
(1)图略.
(2)$\because AB = AC = AD$，$\therefore\triangle BCD$的外接圆圆心为点$A$，半径为$AB$的长.延长$CA$交$\odot A$于点$F$，连结$DF$；$\because AE = 3$，$CE = 1$，$\therefore AF = AC = AE + CE = 4$，$\therefore EF = AE + AF = 7$.$\because\angle CBE = \angle F$，$\angle BEC = \angle FED$，$\therefore\triangle BEC\sim\triangle FED$，$\therefore\frac{BE}{FE}=\frac{CE}{DE}$，$\therefore BE\cdot DE = CE\cdot EF = 7$.本题主要考查了三角形外接圆的作法、圆周角定理、相似三角形的判定与性质，解题的关键是判断出$\triangle BCD$外接圆圆心为点$A$.

22. (10分)网络销售已经成为一种比较热门的销售方式,某电商购进一种单价30元的商品.为减少库存,未来30天,这种商品将开展“每天降价1元”的促销活动,即从活动开始的第1天起,每天的销售单价均比前一天降1元. 通过市场调研发现,该商品的销售单价每降1元,每天销量增加3件. 活动前的销售单价为100元,每天销售15件. 设活动开始后的第$t$天($t$为正整数)所获的利润为$w$(元).
(1) 求出$w$与$t$之间的函数解析式;
(2) 哪一天所获利润最大? 最大利润是多少元?
(3) 若每销售一件商品需缴纳电商平台推广费用$a$元($a＞0$). 在这30天内,要使每天缴纳电商平台推广费用后的利润随着$t$的增大而增大,求$a$的取值范围.

答案： 解:
(1)由题意，得$w=(100 - 30 - t)(15 + 3t)=-3t^2 + 195t + 1050(0\lt t\leqslant30$且$t$为正整数).
(2)$\because - 3\lt0$，且$w$所对应的抛物线对称轴为直线$t = -\frac{195}{2\times(-3)} = 32.5$，$\therefore$当$0\lt t\leqslant30$时，$w$随$t$的增大而增大，$\therefore$当$t = 30$时，$w_{max}=4200$，即在第30天所获利润最大，最大利润为4200元.
(3)由题意，得$w=(100 - 30 - t - a)(15 + 3t)=-3t^2+(195 - 3a)t + 1050 - 15a$.$\because - 3\lt0$，$\therefore$要使每天缴纳电商平台推广费用后的利润随着$t$的增大而增大，则$-\frac{195 - 3a}{2\times(-3)}\gt29.5$，解得$a\lt6$.又$\because a\gt0$，$\therefore0\lt a\lt6$.本题主要考查一次函数与二次函数的实际应用，
(3)为易错题，在利用二次函数的增减性讨论抛物线对称轴的位置时，需结合$t$为正整数这一实际情况分析，因此$-\frac{195 - 3a}{2\times(-3)}\gt29.5$即可满足题意，而非$-\frac{195 - 3a}{2\times(-3)}\geqslant30$.