《2024年孟建平单元测试九年级数学全一册浙教版》

17. (6分)已知抛物线$y = -x^{2}+ax + b$经过点$A(1,0)$，$B(0,-4)$.
(1)求抛物线的解析式；
(2)求此抛物线与坐标轴的三个交点连结而成的三角形的面积.

答案： 解:
(1)由题意,得$\begin{cases}{-1+a+b=0 } \\ {b=-4} \end{cases}$
解得a=5,b=-4
∴抛物线的解析式是y=−x²+5x−4.　　
(2)在y =−x²+5x−4中,
令y=0,解得x1=4,x2=1,
∴抛物线与x轴的另一个交点C(4,0),
∵A(1,0),
∴AC=3.
∵B(O,−4),
∴抛物线与坐标轴的三个交点连结而成的三角形的面积S=$\frac{1}{2}$×3×4=6.

18. (6分)一个不透明的袋子中装有四个小球，上面分别标有数字-2，-1，0，1，它们除数字不同外，其他完全相同.
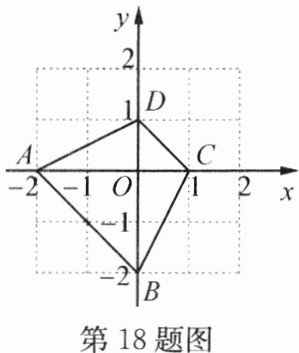
(1)随机从袋子中摸出一个小球，摸出的球上面标的数字为正数的概率是_______；
(2)小聪先从袋子中随机摸出一个小球，记下数字作为平面直角坐标系内点$M$的横坐标；然后放回搅匀. 接着小明从袋子中随机摸出一个小球，记下数字作为点$M$的纵坐标. 如图，已知四边形的四个顶点的坐标分别为$A(-2,0)$，$B(0,-2)$，$C(1,0)$，$D(0,1)$，求点$M$落在四边形$ABCD$内部(含边界)的概率.

答案：
解:
(1)$\frac{1}{4}$　　
(2)列表如下:
　
由表知，共有16种等可能的结果，
其中点M落在四边形ABCD内部(含边界)的有(−2,0),(−1,−1),(−1,0),(0,−2),(0,−1),(0,0),(0,1),(1,0),共8个,
∴点M落在四边形ABCD内部(含边界)的概率为$\frac{1}{2}$.

19. (8分)苍溪独特的土壤、水分、气候组成的生态系统，成为猕猴桃的乐土，被国家誉为“红心猕猴桃第一县、红心猕猴桃之乡”. 某水果店销售红心猕猴桃，平均每天可售出120箱，每箱盈利60元. 为了扩大销售，水果店决定采取适当的降价措施，经调查发现，每箱红心猕猴桃每降价5元，水果店平均每天可多售出20箱. 设每箱红心猕猴桃降价$x$元，每天销售该红心猕猴桃的总利润为$w$元.
(1)求$w$与$x$之间的函数解析式；
(2)试判断总利润能否达到8200元，如果能达到，求出此时$x$的值；如果达不到，求出$w$的最大值.

答案： 解:
(1)由题意,得w与x之间的函数解析式为w=(60−x)(120+$\frac{x}{5}$×20)=−4x²+120.x+7200.
(2)总利润w不能达到8200元.　理由如下:w=−4x²+120x+7200=−4(x−15)²+8100,
∵−4 ＜0,
∴当x=15时,w取到最大值，为8100,
∵8100＜8200,
∴w不能达到8200元,w的最大值是8100.