《2024年孟建平单元测试九年级数学全一册浙教版》

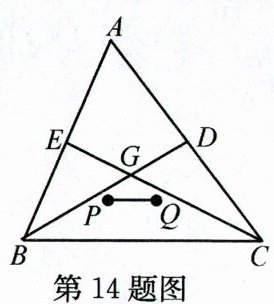
14. 如图,G是△ABC的重心,延长BG交AC于点D,延长CG交AB于点E,P,Q分别是△BCE和△BCD的重心.若BC长为12,则PQ的长为______.

答案： 解析;延长EP交BC于点F,连结DF,DE.
∵点P是△BCE的重心,
∴$\frac{P}{EF}$=$\frac{1}{3}$,F为BC的中点,
∵点Q是△BCD的重心,
∴点Q在线段DF上，
∴FQ$\frac{1}{3}$,
∴$\frac{P}{EF}$=FFDQ=$\frac{1}{3}$,又
∵∠PFQ=
　　　∠EFD,,
∴△PFQ∽△EFD,,
∴EPDQ−$\frac{P}{EF}$=$\frac{1}{3}$.
∵点G是△ABC的重心,
∴BD,CE是△ABC的中线,
∴DE是△ABC的中位线，
∴DE=$\frac{1}{2}$BC=6,
∴P6Q=$\frac{1}{3}$,解得PQ=2.　　点评:本题主要考查重心的性质、相似三角形的判定与性质及三角形中位线定理，解题的关键是灵活运用重心的概念以及重心分三角形的中线成1;2的两条线段.

15. 我们把顶角互补的两个等腰三角形叫做“友好三角形”.在△ABC中,AB=AC=10,点D,E都在边BC上,AD=AE=5.如果△ABC与△ADE是“友好三角形”,那么BC的长为______.

答案：
解析:如图,过点A作AF⊥BC于点F.
∵AB=AC,AD=AE,
∴
DF=EF,BF=CF,∠DAF=∠EAF,∠BAF=∠CAF;
∵△ABC与
　　　△ADE是“友好三角形”,
∴∠BAC+∠DAE=180°,
∴2∠BAF+
　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 2∠DAF=180°,
∴∠BAF+∠DAF=90°,
∵∠BAF+∠B=90°,
∴
∠DAF=∠B,又
∵∠AFD=∠BFA=90°,
∴△FAD∽△FBA,
∴$\frac{A}{BF}$=$\frac{DF}{AF}$=$\frac{AD}{BA}$=$\frac{5}{10}$=$\frac{1}{2}$.设DF =EF=x,则AF=2x,BF=4.x.
∵在Rt△ABF中,AB2=AF²+BF²,
∴10²=(2x)²+(4x)²,解得x =√5(负值已舍),
∴BC=2BF=8x=8$\sqrt{5}$　　点评:本题属于新定义题，主要考查相似三角形的判定与性质，解题的关键是理解“友好三角形”的定义，根据题意画出大致图形，添加等腰三角形中常用的辅助线(作高线)，得到一组相似的直角三角形,利用相似三角形的性质及勾股定理求解.

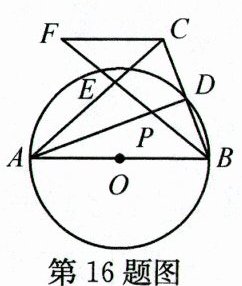
16. 如图,在△ABC中,AB=AC,以AB为直径的⊙O交BC于点D,连结AD,P是AD上一点,过点C作CF//AB,延长BP交AC于点E,交CF于点F.若PE=4,EF=5,则BP=______.

答案： 解析:设⊙O的半径为r,BP=x.延长FC,AD交于点G.
∵AB是⊙O的直径,
∴∠GDC=
　　　∠ADB=90°,
∵AB=AC,
∴CD=BD,
∵CF//AB,
∴∠CGD=∠BAD,
∴△CGD≌△BAD,
∴GC =AB=2r.
∵CF//AB,
∴△CFE∽△ABE,△GFP∽△ABP,
∴$\frac{E}{EB}$　$\frac{CF}{AB}$,$\frac{GF}{AB}$=$\frac{FP}{BP}$,即$\frac{5}{x+4}$=$\frac{CF}{2r}$,$\frac{CF+2}{2r}$=$\frac{9}{x}$,
∴CF=$\frac{10r}{+4}$=$\frac{18r−2rx}{x}$,整理,得x²=36,
∴x=6(负值已舍),即BP=6.　　点评:本题主要考查了圆周角的性质、等腰三角形的性质、全等三角形及相似三角形的判定与性质，难度较大，解题的关键是添加辅助线构造全等三角形和相似三角形，利用相似三角形对应边成比例列方程求解.

17. (6分)如图,在8×8的正方形网格中,每个小正方形的边长都为1,点$A,B,C$均在格点上,请按要求在网格中画图,所画图形的顶点均需在格点上.
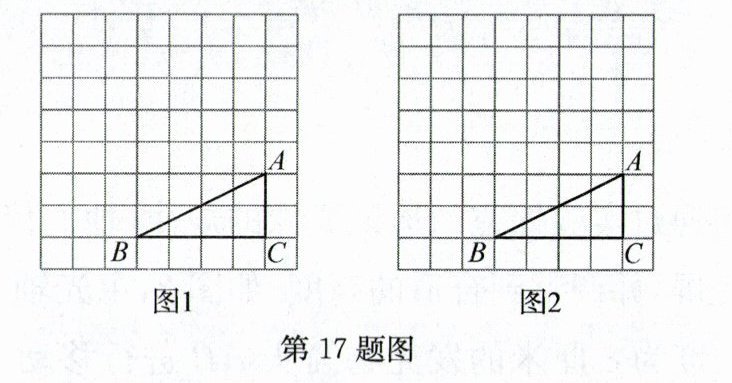
(1) 在图1中以线段$AB$为边画一个$△ABD,$使其与$△ABC$相似,但不全等;
(2) 在图2中画一个$△EFG,$使其与$△ABC$相似,且周长为$△ABC$的2倍.

答案： 解:图略.

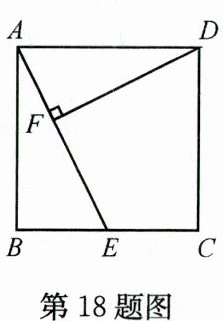
18. (6分)如图,正方形ABCD中,AB=2,E是BC的中点,DF⊥AE于点F.
(1) 试说明△ABE∽△DFA;
(2) 求△DFA的面积S₁和四边形CDFE的面积S₂.

答案： 解:
(1)
∵在正方形ABCD中,∠B=∠BAD=90°,
∴∠BAE+∠AEB=∠BAE+∠DAF=90°,
∴∠AEB=∠DAF,又
∵∠B=∠DFA=90°,
∴△ABE∽△DFA,　　
(2)由
(1)可知SSABE=($\frac{AE}{AD}$2,
∵BC=AD=AB=2,E是BC的中点,
∴BE=$\frac{1}{2}$BC=1,
∵∠B=90°,
∴SABE=$\frac{1}{2}$AB.BE=1,
AE=√AB²+BE²=$\sqrt{5}$,
∴$\frac{1}{S}$=($\frac{\sqrt{5}}{2}$)2
∴S=$\frac{4}{5}$,
∴S2=S正方形ABCD−S−SABE=4−$\frac{4}{5}$−1=$\frac{11}{5}$.

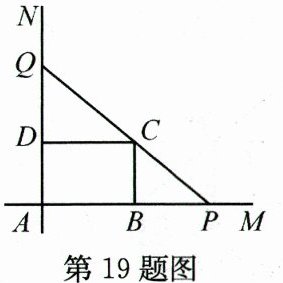
19. (8分)如图,互相垂直的两条公路AM,AN旁有一矩形花园ABCD,其中AB=30米,AD=20米.现欲将其扩建成一个三角形花园APQ,要求P在射线AM上,Q在射线AN上,且PQ经过点C.
(1) 当DQ=10米时,求△APQ的面积;
(2) 当DQ的长为多少米时,△APQ的面积为1600平方米?

答案： 解:
(1)
∵AD=20米,DQ=10米,
∴AQ=AD+DQ=30(米).
∵在矩形ABCD中,DC=AB=30 米,DC//AB,
∴AQ　$\frac{DC}{P}$,即$\frac{10}{30}$=$\frac{30}{AP}$,解得AP=90米，
∴SAPQ　$\frac{1}{2}$AQ.AP=1350平方米.
(2)设DQ=x米,则AQ|(z+20))米,由
(1)得岩$\frac{DC}{AP}$,即$\frac{x}{+20}$=$\frac{30}{AP}$
∴AP=$\frac{30(x+20)}{x}$.由题意,得S△APQ=$\frac{1}{2}$×　　x　　×(x+20)=1600,化简,得3.x²−200x+1200=0,解得x=60或$\frac{20}{3}$.
　　　经检验，r=60或$\frac{20}{3}$是原方程的根，且符合题意，
∴当DQ的长为60或$\frac{20}{3}$米时,△APQ的面积为1600平方米.