《2024年孟建平单元测试九年级数学全一册浙教版》

15. 图1是“中国第一泉”鸣沙山月牙泉,其示意图如图2,它是由$\overset{\frown}{ADB}$和$\overset{\frown}{ACB}$组成的封闭图形,C,D分别为$\overset{\frown}{ACB}$和$\overset{\frown}{ADB}$的中点,测得∠ADB=30°,∠ACB=45°.记$\overset{\frown}{ACB}$所在圆的半径为r米,$\overset{\frown}{ADB}$所在圆的半径为R米,则$\frac{r}{R}=$______.若测得AB为50米,则C,D两点之间的距离为______米.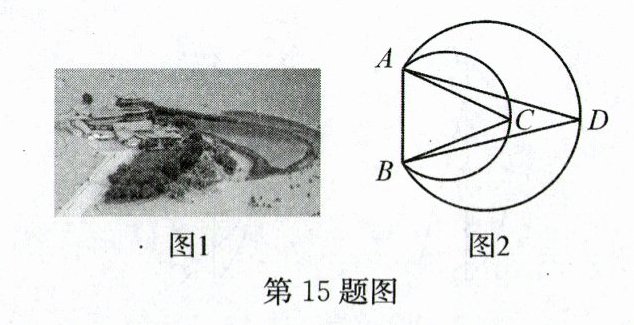

答案：
$\frac{\sqrt{2}}{2}$　25+25$\sqrt{3}$−25$\sqrt{2}$　解析:如图，设ACB所在圆的圆心为O,ADB所在圆
　　　的圆,心为O2,易得O,O,C,D四点共线,连结OD,AO,BO,AO,BO,则
AO=BO=r,AO=BO=R.
∵∠ACB=45°,∠ADB=30°,
∴∠AOB=
　　　2∠ACB=90°,∠AOB=2∠ADB=60°,
∴△AOB是等腰直角三角形,△AOB
　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 是等边三角形，
∴AB=√AO+BO=$\sqrt{2}$r,AB=AO=R,
∴$\sqrt{2}$r=R,
∴$\frac{r}{R}$=
　　　$\frac{\sqrt{2}}{2}$.当AB=50,即　　$\sqrt{2}$r=50时,解得r=25$\sqrt{2}$
∴R=50,
∴00=$\frac{\sqrt{3}}{2}$R−$\frac{\sqrt{2}}{2}$r=
　　　25$\sqrt{3}$−25,
∴CD=0D−0C=0O+OD−OC=(25+25$\sqrt{3}$−25$\sqrt{2}$)米.

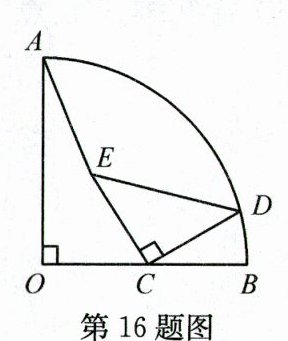
16. 如图,$\overset{\frown}{AB}$所对圆心角∠AOB=90°,半径为8,C是OB的中点,D是$\overset{\frown}{AB}$上一点,CD绕点C逆时针旋转90°得到CE,则AE的最小值是______.

答案：
4$\sqrt{10}$−8　解析:如图，连结OD,以OC为边向下作正方形OCTH，连结AT,ET.
　
∵OA=OB=8,C是OB的中点,
∴CT=HT=OH=CO=4,
∴AH=AO+OH=
　　　12,
∴AT=　$\sqrt{AH+HT²}$=4　$\sqrt{10}$
∵∠OCT=∠ECD=90°,
∴∠OCD=∠TCE.
　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　
CO=CT,
　　　在△OCD和△TCE中,∠OCD=∠TCE,
∴△OCD≌△TCE,
∴TE=OD=8,
∴
CD=CE,
　　　　　　　　　　　　{
AE≥AT−TE=4$\sqrt{10}$−8(当且仅当A,E,T三点共线时,等号成立),
∴AE的最小值为4$\sqrt{10}$−8.

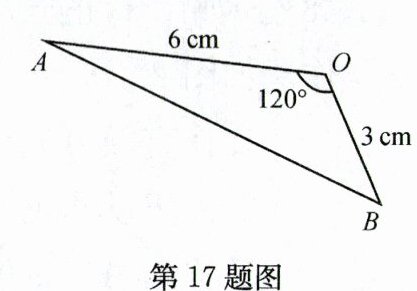
17. (6分)考古人员欲将一出土的扇形饰物复原,O是扇形的圆心,OA为半径,测得剩余部分△AOB的边长、角的大小如图所示,则应补充多大面积才能复原?

答案： 解:过点A作AC⊥BO的延长线于点C,则∠C=90o.
∵∠AOB=120°,
∴∠AOC=60°,
∴∠CAO=
　　　180°−C−∠AOC==330o°,
∴oc=$\frac{1}{2}$OA=3cm,
∴AC=3$\sqrt{3}$cm,
∴S扇形−SAOB=$\frac{120π×6²}{360}$−$\frac{1}{2}$×3×3$\sqrt{3}$=(12π−$\frac{9}{2}$$\sqrt{3}$)cm²,即应补充(12π−$\frac{9}{2}$$\sqrt{3}$)cm²才能复原.

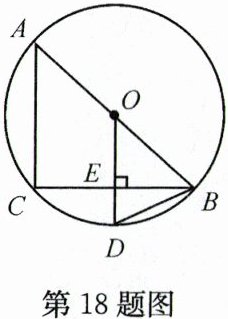
18. (6分)如图,AB是⊙O的直径,BC是弦,OD⊥BC于点E,交$\overset{\frown}{BC}$于点D.
(1) 请写出四个不同类型的正确结论;
(2) 连结CD,设∠CDB=α,∠ABC=β,试找出α与β之间的一种等量关系式并给予证明.

答案：
(1)解:①BE=CE;②BD=CD;③∠BED=90°;④∠BOD=∠A;⑤AC//OD;⑥AC⊥BC等等.(答9案0°不−唯∠一AB,写C=出9四0°个−即β.可
∵)A,B(2,D)α,一Cβ四=点90共°.圆，证
∴∠明A:
∵+A∠BC是DB⊙=O1的80°直,即径9，0
∴°−∠βA+CαB==18900°°,,
∴
∴α∠−Aβ==
　19.9解0°:.