《2024年数学学习与巩固五年级上册北师大版》

3. 判断。(对的画“√”,错的画“×”。)
(1)在一个长方形内画一个最大的三角形,这个三角形的面积等于长方形面积的一半。(√)
(2)当梯形的上底和下底一定时,梯形越高,它的面积就越大。(√)
(3)一个三角形底扩大为原来的 $2$ 倍,高缩小为原来的 $\frac{1}{2}$,面积不变。(√)
(4)计算的面积,只能把它分成一个三角形和一个长方形来计算。(×)
(5)如图所示,计算涂色部分的面积,可以用长方形的面积减去梯形的面积。(√)

答案： （1）√
（2）√
（3）√
（4）×
（5）√

4. 估计下面图形的面积。(每个小方格的面积表示 $1cm^{2}$。)

- 面积约为(10)
- 面积约为(14)
- 面积约为(12)

答案： - 10
14
12

5. 计算下面图形的面积。

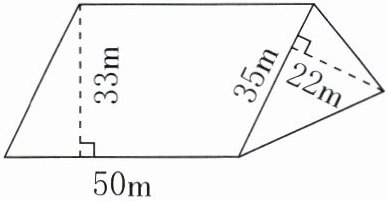
答案： 该图形的面积为$2035$平方米。

6. 计算下面图形中涂色部分的面积。(单位：$dm$)

-
-

答案： 第一幅图
涂色部分面积=大正方形面积+小正方形面积-上面三角形面积
$6×6 + 3.5×3.5-\frac{1}{2}×6×(6 + 3.5)$
$=36+12.25 - 28.5$
$=29.75(dm^{2})$
第二幅图
梯形面积为$(8 + 8÷2)×8÷2=48(dm^{2})$
空白大三角形面积为$\frac{1}{2}×8×8 = 32(dm^{2})$
涂色部分面积为$48-32 = 16(dm^{2})$
综上，答案依次为$29.75dm^{2}$；$16dm^{2}$。