第53页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
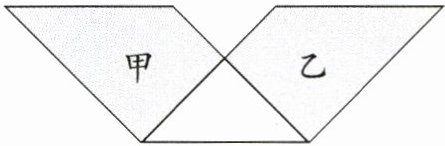
下图中甲、乙两部分的面积大小一样吗? 说明理由。

答案:
甲、乙两部分面积一样大。
理由:甲和乙所在的两个平行四边形等底等高,根据平行四边形面积公式(面积=底×高),两平行四边形面积相等。两平行四边形重叠部分面积相同,故甲的面积=平行四边形面积-重叠部分面积,乙的面积=平行四边形面积-重叠部分面积,因此甲和乙面积相等。
理由:甲和乙所在的两个平行四边形等底等高,根据平行四边形面积公式(面积=底×高),两平行四边形面积相等。两平行四边形重叠部分面积相同,故甲的面积=平行四边形面积-重叠部分面积,乙的面积=平行四边形面积-重叠部分面积,因此甲和乙面积相等。
1. 填表。
|平行四边形的底|底对应的高|平行四边形的面积|
|8cm|4.2cm| |
|9.8dm| |$78.4dm^2$|
| |20.2m|$505m^2$|

|平行四边形的底|底对应的高|平行四边形的面积|
|8cm|4.2cm| |
|9.8dm| |$78.4dm^2$|
| |20.2m|$505m^2$|

答案:
表格从左到右依次填$33.6cm^{2}$;$8dm$;$25m$。
2. 选择。(把正确答案的序号填在括号里。)
(1)将平行四边形的框架拉成一个长方形,它的周长(
①比原来大 ②比原来小 ③和原来相等
(2)平行四边形的底扩大到原来的3倍,底对应的高不变,面积(
①扩大到原来的3倍 ②缩小到原来的$\frac{1}{3}$ ③不变
(1)将平行四边形的框架拉成一个长方形,它的周长(
③
),面积(①
)。①比原来大 ②比原来小 ③和原来相等
(2)平行四边形的底扩大到原来的3倍,底对应的高不变,面积(
①
)。①扩大到原来的3倍 ②缩小到原来的$\frac{1}{3}$ ③不变
答案:
(1)③;①
(2)①
(1)③;①
(2)①
3. 如图,在一块平行四边形的草地中有一条长16m、宽2m的小路,求草地的面积。


答案:
由图可知小路为平行四边形,其底为$2m$,高为$16m$(小路长),那么小路面积为$2 × 16 = 32$($m^2$)。
大平行四边形底是$36m$,高是$16m$,其面积为$36×16 = 576$($m^2$)。
草地面积等于大平行四边形面积减去小路面积,即$576 - 32 = 544$($m^2$)。
综上,草地面积是$544m^2$。
大平行四边形底是$36m$,高是$16m$,其面积为$36×16 = 576$($m^2$)。
草地面积等于大平行四边形面积减去小路面积,即$576 - 32 = 544$($m^2$)。
综上,草地面积是$544m^2$。
查看更多完整答案,请扫码查看


