《2026年伴你学九年级数学下册苏科版》

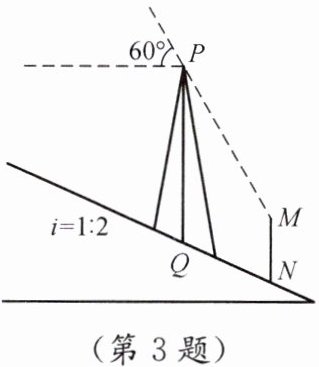
3.如图，信号塔$PQ$坐落在坡度$i$为$1:2$的山坡上，其正前方直立着一警示牌.当太阳光线与水平线成$60^{\circ}$角时，测得信号塔$PQ$落在斜坡上的影子$QN$长为$2\sqrt{5}\ m$，落在警示牌上的影子$MN$长为$3\ m$，求信号塔$PQ$的高.(结果保留根号)

答案：

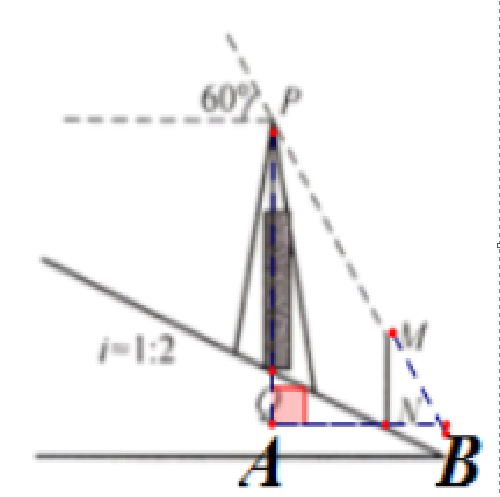
解：过点$N$作平行与地面的直线，与$PQ $延长线相交于点$A，$　　

与$PM$的延长线相交于点$B$　　

由题意可知，$∠MBN=60°$　　

∴$BN=\frac {MN}{tan 60°}=\sqrt{3}m$　　

∵坡度$i=1 $：$ 2$　　

∴$AN=2AQ$　　

∵$AN²+AQ²=QN²$　　

∴$AQ=2m，$$AN=4m$　　

∴$AB= AN+ BN= (4+\sqrt{3})m$　　

∴$AP= tan 60°×AB= (3 + 4\sqrt{3})m$　　

∴$PQ= AP- AQ=(1 + 4\sqrt{3})m$　　

答：信号塔$PQ$上的高为$(1 + 4\sqrt{3})m。$　　

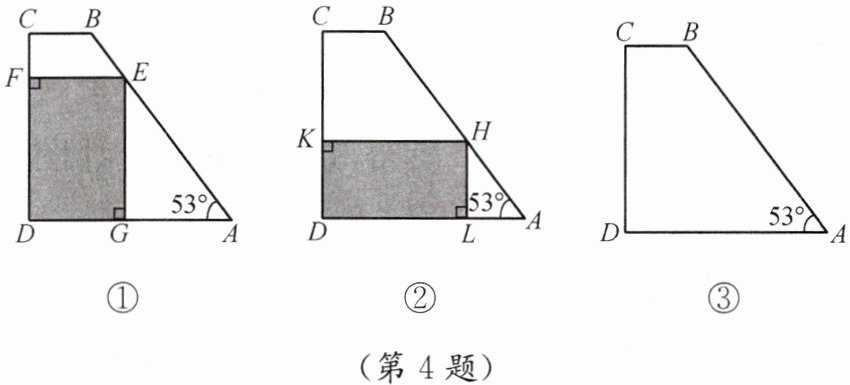
4.小林家门前有一块四边形的空地$ABCD$，其中$AD// BC$，$BC = 1.6\ m$，$AD = 5.5\ m$，$CD = 5.2\ m$，$\angle C = 90^{\circ}$，$\angle A = 53^{\circ}$.小林的爸爸想将一辆长$4.9\ m$、宽$1.9\ m$的汽车停放在这块空地上，让小林算算是否可行.小林设计了两种方案，如图①和图②所示.(参考数据：$\sin 53^{\circ}\approx 0.8$，$\cos 53^{\circ}\approx 0.6$，$\tan 53^{\circ}\approx\frac{4}{3}$)
(1)请你通过计算说明小林的两种设计方案是否合理；
(2)请你利用图③再设计一种有别于小林的可行性方案，并说明理由.

答案：
解:
(1)①当EF= 1.9m时
AG= AD-DG=3.6m
$EG=tan 53°×AG≈4.8m \lt 4.9m$
所以①不可行
②当DL=4.9m时
AL= AD-DL=0.6m
$HL=tan 53°×AL=0.8m\lt 1.9m$
所以②不可行
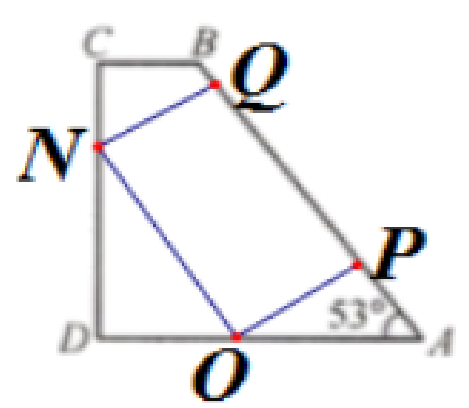
(2)设计方案如图
当AO=2.5m时
$OP=sin 53°×AO≈2m\gt 1.9m$
AP=cos 53°×AO≈1.5m
$AB=\frac{CD}{sin_{53}°}≈ 6.5m$
$PQ=AB-AP=5m\gt 4.9m$
所以此方案可行