第86页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
活动一:知识梳理
1. 本章我们对直角三角形进行了深入的研究,请从以下三个方面归纳$Rt\bigtriangleup ABC$(图 7 - 17)中各元素间的关系:
(1)三边之间的关系:
(2)锐角之间的关系:
(3)边、角之间的关系: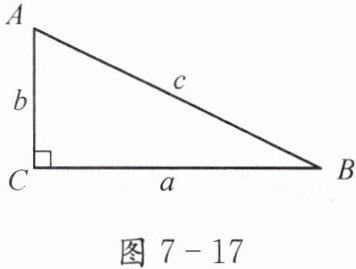
2. 知道直角三角形中的
1. 本章我们对直角三角形进行了深入的研究,请从以下三个方面归纳$Rt\bigtriangleup ABC$(图 7 - 17)中各元素间的关系:
(1)三边之间的关系:
$a^{2}+b^{2}=c^{2}$
;(2)锐角之间的关系:
$\angle A + \angle B = 90^{\circ}$
;(3)边、角之间的关系:
$\sin A = \frac{a}{c}$,$\cos A = \frac{b}{c}$,$\tan A = \frac{a}{b}$ $\sin B = \frac{b}{c}$,$\cos B = \frac{a}{c}$,$\tan B = \frac{b}{a}$
.
2. 知道直角三角形中的
两个元素,其中至少有一个是边
,就可以求出其余元素.
答案:
a²+b²=c²
∠A+∠B=90°
$ sinA=\frac {a}{c},$$cosA=\frac {b}{c},$$tanA=\frac {a}{b}....$
两个元素,其中至少有一个是边
∠A+∠B=90°
$ sinA=\frac {a}{c},$$cosA=\frac {b}{c},$$tanA=\frac {a}{b}....$
两个元素,其中至少有一个是边
活动二:提升认识
1. 结合课本中的图 7 - 5 和图 7 - 8,探索锐角三角函数值的变化规律,并用语言概括.
2. 观察直角三角形中两个锐角的三角函数,探索它们之间的关系.
1. 结合课本中的图 7 - 5 和图 7 - 8,探索锐角三角函数值的变化规律,并用语言概括.
2. 观察直角三角形中两个锐角的三角函数,探索它们之间的关系.
答案:
解:一个锐角的正弦值随角度的增大而增大,余弦值随角度的增大而减小,正切值随角度的增大而增大
解: sinA=cosB;cos A=sin B;tanA×tanB=1
解: sinA=cosB;cos A=sin B;tanA×tanB=1
活动三:典例评析
图 7 - 18,在锐角三角形$ABC$中,$AB = 10\ cm$,$BC = 9\ cm$,$\bigtriangleup ABC$的面积为$27\ cm^2$. 求$\tan B$的值.
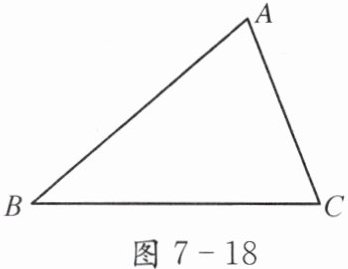
图 7 - 18,在锐角三角形$ABC$中,$AB = 10\ cm$,$BC = 9\ cm$,$\bigtriangleup ABC$的面积为$27\ cm^2$. 求$\tan B$的值.

答案:
解:过点A作AH⊥BC于H
∵${S}_{△ABC}=27\ \mathrm {cm}²$
∴$\frac {1}{2}×9×AH=27$
∴$AH=6\ \mathrm {cm}$
∵$AB=10\ \mathrm {cm},$$AH=6\ \mathrm {cm}$
∴$BH=\sqrt{AB²-AH²}=\sqrt{10²-6²}=8(\ \mathrm {cm})$
∴$tanB=\frac {AH}{BH}=\frac {6}{8}=\frac {3}{4}$
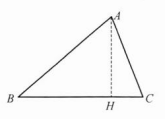
解:过点A作AH⊥BC于H
∵${S}_{△ABC}=27\ \mathrm {cm}²$
∴$\frac {1}{2}×9×AH=27$
∴$AH=6\ \mathrm {cm}$
∵$AB=10\ \mathrm {cm},$$AH=6\ \mathrm {cm}$
∴$BH=\sqrt{AB²-AH²}=\sqrt{10²-6²}=8(\ \mathrm {cm})$
∴$tanB=\frac {AH}{BH}=\frac {6}{8}=\frac {3}{4}$

1. 如图,已知$AB$是$\odot O$的直径,$CD$是$\odot O$的弦,$AB\perp CD$,垂足为$E$. 若$AB = 26$,$CD = 24$,则$\angle OCE$的余弦值为(

A.$\frac{7}{13}$
B.$\frac{12}{13}$
C.$\frac{7}{12}$
D.$\frac{13}{12}$
B
).
A.$\frac{7}{13}$
B.$\frac{12}{13}$
C.$\frac{7}{12}$
D.$\frac{13}{12}$
答案:
B
查看更多完整答案,请扫码查看


