第90页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
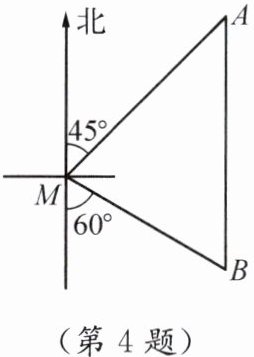
4.如图,一艘渔船位于小岛$M$的北偏东$45^{\circ}$方向、距离小岛$180\ n\ mile$的$A$处,渔船从$A$处沿正南方向航行一段距离后,到达位于小岛南偏东$60^{\circ}$方向的$B$处.
(1)求渔船从$A$处到$B$处的航行过程中与小岛$M$之间的最短距离(用根号表示).
(2)若渔船以$20\ n\ mile/h$的速度从$B$处沿$BM$方向行驶,求渔船从$B$处到达小岛$M$的航行时间.(结果精确到$0.1\ h$;参考数据:$\sqrt{2}\approx 1.41$,$\sqrt{3}\approx 1.73$,$\sqrt{6}\approx 2.45$)
(1)求渔船从$A$处到$B$处的航行过程中与小岛$M$之间的最短距离(用根号表示).
(2)若渔船以$20\ n\ mile/h$的速度从$B$处沿$BM$方向行驶,求渔船从$B$处到达小岛$M$的航行时间.(结果精确到$0.1\ h$;参考数据:$\sqrt{2}\approx 1.41$,$\sqrt{3}\approx 1.73$,$\sqrt{6}\approx 2.45$)

答案:
解:
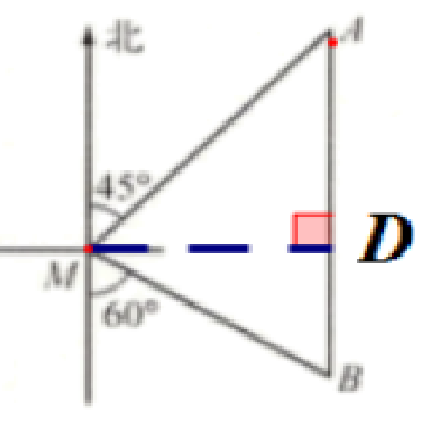
(1)过点M作MD⊥AB ,垂足为点D
$MD= AM · cos 45°= 90\sqrt{2}($海里)
答:渔船从A处到B处的航行过程中与小岛之间的最小距离是$90\sqrt{2}$海里。
(2)因为$MD= 90\sqrt{2}$海里
则$MB=\frac {MD}{cos 30°}= 60\sqrt{6}$
$60\sqrt{6}÷20=3\sqrt{6}≈7.4($时)
答:渔船从B处到达小岛M的航行时间约为7.4时。
解:
(1)过点M作MD⊥AB ,垂足为点D
$MD= AM · cos 45°= 90\sqrt{2}($海里)
答:渔船从A处到B处的航行过程中与小岛之间的最小距离是$90\sqrt{2}$海里。
(2)因为$MD= 90\sqrt{2}$海里
则$MB=\frac {MD}{cos 30°}= 60\sqrt{6}$
$60\sqrt{6}÷20=3\sqrt{6}≈7.4($时)
答:渔船从B处到达小岛M的航行时间约为7.4时。

1.如图,已知$\triangle ABC$内接于半径为$1$的$\odot O$,$\angle BAC=\theta$($\theta$是锐角),则$\triangle ABC$的面积的最大值为(

A.$\cos\theta(1 + \cos\theta)$
B.$\cos\theta(1+\sin\theta)$
C.$\sin\theta(1+\sin\theta)$
D.$\sin\theta(1+\cos\theta)$
D
).
A.$\cos\theta(1 + \cos\theta)$
B.$\cos\theta(1+\sin\theta)$
C.$\sin\theta(1+\sin\theta)$
D.$\sin\theta(1+\cos\theta)$
答案:
D
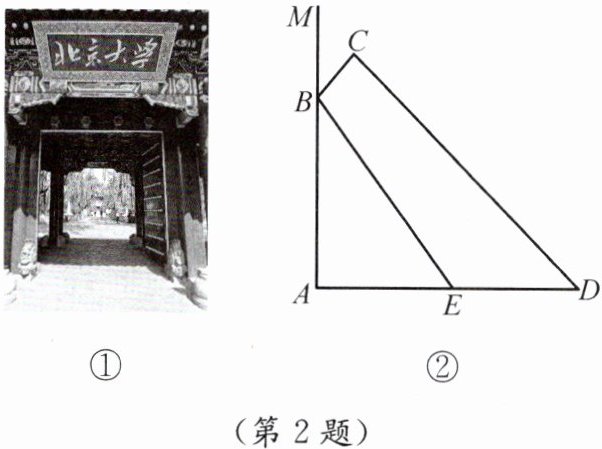
2.如图①,我国传统建筑的大门上常常悬挂着巨大的匾额.如图②,线段$BC$是悬挂在墙壁$AM$上的某块匾额.已知$BC = 1\ m$,$\angle MBC = 37^{\circ}$.从水平地面点$D$处看点$C$的仰角$\angle ADC = 45^{\circ}$,从点$E$处看点$B$的仰角$\angle AEB = 53^{\circ}$,且$DE = 2.4\ m$.(参考数据:$\sin 37^{\circ}\approx\frac{3}{5}$,$\cos 37^{\circ}\approx\frac{4}{5}$,$\tan 37^{\circ}\approx\frac{3}{4}$)
(1)求点$C$到墙壁$AM$的距离;
(2)求匾额悬挂的高度$AB$.
(1)求点$C$到墙壁$AM$的距离;
(2)求匾额悬挂的高度$AB$.

答案:
2. 解:
(1)过点C作CF⊥AM,垂足为点F
∴CF=sin∠FBC×BC≈0.6m
(2)过点C作CG⊥AD,垂足为点G
∵∠AEB= 53°
∴∠ABE=90°-53°= 37°
∴AE= tan 37°×AB=\frac {3}{4}x
∵∠ADC=45°
∴CG= DG
∵CG=AB+ BF
∴x+0.8=\frac {3}{4}x+1.8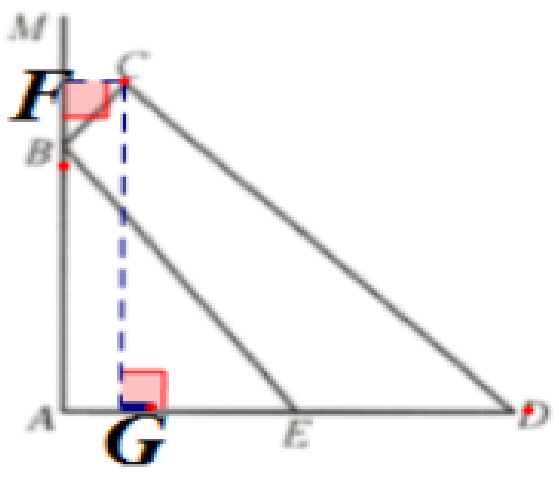
2. 解:
(1)过点C作CF⊥AM,垂足为点F
∴CF=sin∠FBC×BC≈0.6m
答:点C到墙壁AM的距离为0.6m。
(2)过点C作CG⊥AD,垂足为点G
设AB=xm
由
(1)知,BF=cos 37°×BC≈0.8m
(1)知,BF=cos 37°×BC≈0.8m
∵∠AEB= 53°
∴∠ABE=90°-53°= 37°
∴AE= tan 37°×AB=\frac {3}{4}x
DG= AE+ DE- CF=\frac {3}{4}x+ 1.8
∵∠ADC=45°
∴CG= DG
∵CG=AB+ BF
∴x+0.8=\frac {3}{4}x+1.8
答:匾额悬挂高度AB为4m。

查看更多完整答案,请扫码查看


