第65页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
活动一:操作思考
1. 正切是如何定义的?
2. 阅读课本中的“观察与思考”并填写表格.
(1)观察表格中正切值的变化,你发现了什么规律?
(2)根据正切的定义,结合课本图 7-8 中各锐角的终边与过点(1,0)且垂直于 x 轴的直线的交点的变化,你能发现各角的正切值随着角度变化有什么变化吗?
3. 阅读课本中的例 3,学会用计算器求一个锐角的正切值.任取一些锐角(不同于问题 2 表格中的角),用计算器计算它们的正切值,验证问题 2 中发现的规律是否正确.
1. 正切是如何定义的?
2. 阅读课本中的“观察与思考”并填写表格.
(1)观察表格中正切值的变化,你发现了什么规律?
(2)根据正切的定义,结合课本图 7-8 中各锐角的终边与过点(1,0)且垂直于 x 轴的直线的交点的变化,你能发现各角的正切值随着角度变化有什么变化吗?
3. 阅读课本中的例 3,学会用计算器求一个锐角的正切值.任取一些锐角(不同于问题 2 表格中的角),用计算器计算它们的正切值,验证问题 2 中发现的规律是否正确.
答案:
解:在直角三角形中,锐角A的正切$tanA =\frac {∠A的对边}{∠A的邻边}$
解: tanθ的值随θ的增大而增大。
解:随着锐角的增大,其正切值也增大。
解: tan 15°≈0.27;tan 35°≈0.70;tan 55°≈1.43
规律正确
解: tanθ的值随θ的增大而增大。
解:随着锐角的增大,其正切值也增大。
解: tan 15°≈0.27;tan 35°≈0.70;tan 55°≈1.43
规律正确
活动二:探究发现
1. 计算下列各组锐角的正切值.
(1)$30°$和$60°$;(2)$26.6°$和$63°24'$;
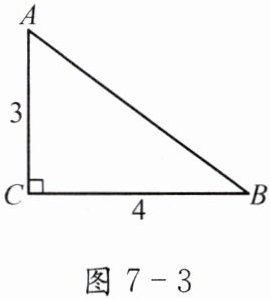
2. 如图 7-3,求$\tan A$和$\tan B$.
3. 观察问题 1、2 中的计算结果,你发现了什么规律?证明你的发现.
1. 计算下列各组锐角的正切值.
(1)$30°$和$60°$;(2)$26.6°$和$63°24'$;
2. 如图 7-3,求$\tan A$和$\tan B$.

3. 观察问题 1、2 中的计算结果,你发现了什么规律?证明你的发现.
答案:
解:$ (1)tan 30°=\frac {\sqrt{3}}{3};$$tan 60°=\sqrt{3}$
(2)tan 26.6°≈0.5;tan 63°24'≈2
解:$tanA=\frac {BC}{AC}=\frac {4}{3}$
$tanB=\frac {AC}{BC}=\frac {3}{4}$
解:发现当∠A+∠B=90°时,tan A×tan B=1
$tanA×tanB=\frac {∠A的对边}{∠A的邻边}×\frac {∠A的邻边}{∠A的对边}=1$
(2)tan 26.6°≈0.5;tan 63°24'≈2
解:$tanA=\frac {BC}{AC}=\frac {4}{3}$
$tanB=\frac {AC}{BC}=\frac {3}{4}$
解:发现当∠A+∠B=90°时,tan A×tan B=1
$tanA×tanB=\frac {∠A的对边}{∠A的邻边}×\frac {∠A的邻边}{∠A的对边}=1$
查看更多完整答案,请扫码查看


