第23页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
活动一:想一想 说一说
阅读课本“问题1”并思考:
(1)① 你从问题1中获得了哪些信息?
② 在这些信息中,包含了哪些数量的信息?
③ 这些数量之间有什么关系?
④ 你能运用什么方法来描述这些数量之间的关系?
(2)设总收益为$y$(元),尝试写出$y$(元)与$x$(亩)之间的函数表达式:
(3)该种粮大户今年应新承租多少亩稻田才能使总收益最大?
阅读课本“问题1”并思考:
(1)① 你从问题1中获得了哪些信息?
② 在这些信息中,包含了哪些数量的信息?
③ 这些数量之间有什么关系?
④ 你能运用什么方法来描述这些数量之间的关系?
(2)设总收益为$y$(元),尝试写出$y$(元)与$x$(亩)之间的函数表达式:
y=440×360+(440 - 2x)x
.(3)该种粮大户今年应新承租多少亩稻田才能使总收益最大?
答案:
y=440×360+(440-2x)x
解:
(1)①获得去年种植水稻亩数及其平均每亩收益;今年每新承租亩数与平均每亩收益的关系。
②包含了获得去年种植360亩水稻,平均每亩收益440元;今年每新承租1亩,平均每亩收益少2元。
③收益总值=水稻亩数x平均每亩收益平均每亩收益=440-2×新承租亩数
④用函数表达式来进行描述
(3)y=-2(x-110)²+182600
当x=-110时,y的值最大,最大值是182600
答:该种粮大户今年应多承租110亩稻田,才能使总收益最大,最大收益为182600元。
解:
(1)①获得去年种植水稻亩数及其平均每亩收益;今年每新承租亩数与平均每亩收益的关系。
②包含了获得去年种植360亩水稻,平均每亩收益440元;今年每新承租1亩,平均每亩收益少2元。
③收益总值=水稻亩数x平均每亩收益平均每亩收益=440-2×新承租亩数
④用函数表达式来进行描述
(3)y=-2(x-110)²+182600
当x=-110时,y的值最大,最大值是182600
答:该种粮大户今年应多承租110亩稻田,才能使总收益最大,最大收益为182600元。
活动二:做一做,算一算
如图5-8,某跳水运动员在进行跳水训练时,身体(可看成一点)在空中的运动轨迹近似看成一条抛物线.已知跳板$AB$长为$4.8{m}$,跳板距离水面$CD$的高度$BC$为$3{m}$.训练时,运动员在离起跳点$A$的水平距离为$1{m}$处达到距离水面的最大高度$4{m}$.以$CD$为横轴,$CB$为纵轴建立平面直角坐标系.
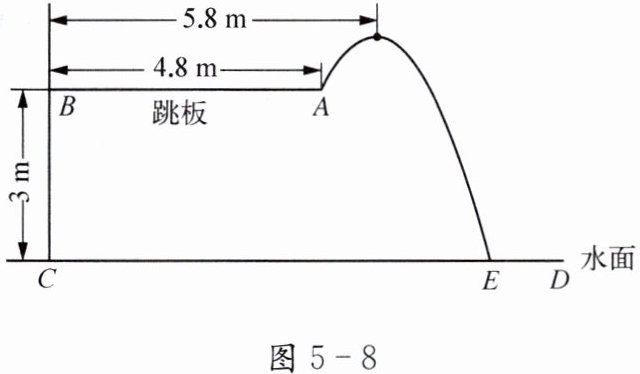
(1)求这条抛物线相应的函数表达式;
(2)求运动员落水点$E$与点$C$的距离.
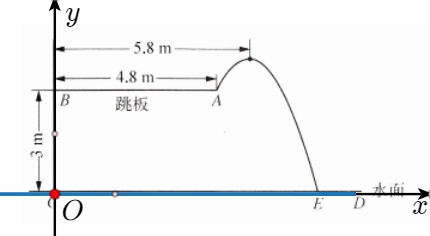
如图5-8,某跳水运动员在进行跳水训练时,身体(可看成一点)在空中的运动轨迹近似看成一条抛物线.已知跳板$AB$长为$4.8{m}$,跳板距离水面$CD$的高度$BC$为$3{m}$.训练时,运动员在离起跳点$A$的水平距离为$1{m}$处达到距离水面的最大高度$4{m}$.以$CD$为横轴,$CB$为纵轴建立平面直角坐标系.

(1)求这条抛物线相应的函数表达式;
(2)求运动员落水点$E$与点$C$的距离.
答案:
解:
(2)
∵y=-(x -5.8)²+4
∴令y=0得0=-(x-5.8)²+ 4
解得${x}_1= 7.8,$${x}_2=3.8$
∵起跳点A坐标为(4.8,3)
∴${x}_1=3.8$不符合题意
∴x=7.8
∴运动员落水点E与点C的距离为7.8m

解:
(2)
∵y=-(x -5.8)²+4
∴令y=0得0=-(x-5.8)²+ 4
解得${x}_1= 7.8,$${x}_2=3.8$
∵起跳点A坐标为(4.8,3)
∴${x}_1=3.8$不符合题意
∴x=7.8
∴运动员落水点E与点C的距离为7.8m
查看更多完整答案,请扫码查看


