第39页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
活动四:想一想 试一试
1. 思考课本中的“尝试与交流”,想一想:如何判断两个矩形为相似矩形?两个菱形呢?
2. 如何判定两个多边形为相似多边形?
1. 思考课本中的“尝试与交流”,想一想:如何判断两个矩形为相似矩形?两个菱形呢?
2. 如何判定两个多边形为相似多边形?
答案:
解: 看矩形的边是否都对应成比例,看菱形的角是否都对应相等。
解:看边是否对应成比例,看角是否都对应相等。
解:看边是否对应成比例,看角是否都对应相等。
1. 下列说法中,错误的是(
A.全等图形一定是相似图形
B.两个等边三角形一定相似
C.两个等腰直角三角形一定相似
D.两个直角三角形一定相似
D
).A.全等图形一定是相似图形
B.两个等边三角形一定相似
C.两个等腰直角三角形一定相似
D.两个直角三角形一定相似
答案:
D
2. 填空:
(1) 如果△ABC∽△DEF,∠A = 60°,∠B = 40°,那么△DEF 中最小角的度数为
(2) △ABC 的三条边长分别为 6、8、10,与其相似的△DEF 的最短边的长为 3,则△DEF 的
最长边的长为
(1) 如果△ABC∽△DEF,∠A = 60°,∠B = 40°,那么△DEF 中最小角的度数为
$40^{\circ}$
.(2) △ABC 的三条边长分别为 6、8、10,与其相似的△DEF 的最短边的长为 3,则△DEF 的
最长边的长为
5
.
答案:
40°
5
5
3. 如图,五边形 ABCDE∽五边形 RSTUV,求∠R 的度数和边 RS 的长.


答案:
解:
∵五边形ABCDE∽五边形RSTU{V }
∴∠R=∠A=128°,$\frac {AB}{RS}=\frac {AE}{RV}$
∴$\frac {4}{RS}=\frac {6}{4}$
∴$RS=\frac {8}{3}$
∵五边形ABCDE∽五边形RSTU{V }
∴∠R=∠A=128°,$\frac {AB}{RS}=\frac {AE}{RV}$
∴$\frac {4}{RS}=\frac {6}{4}$
∴$RS=\frac {8}{3}$
1. 如图,在□ABCD 中,AC 与 BD 相交于点 O,F、E、M、N 分别是 AO、BO、CO、DO 的中点,连
接 FE、EM、MN、FN,得到□FEMN.
求证:□ABCD∽□FEMN.

接 FE、EM、MN、FN,得到□FEMN.
求证:□ABCD∽□FEMN.

答案:
证明:
∵点F、E、M、N分别是AO、BO、CO、DO的中点
∴EF 是△AOB的中位线,FN是△AOD的中位线,
MN是△COD的中位线,EM是△BOC的中位线
∴EF//AB,FN//AD,
$\frac {EF}{AB}=\frac {FN}{AD}=\frac {MN}{CD}=\frac {EM}{BC}=\frac {1}{2}$
∵EF//AB,FN//AD
∴∠EFO=∠BAO,∠NFO=∠DAO
∴∠EFN=∠BAD
同理可得:∠FNM=∠ADC,∠NME=∠DCB,∠MEF=∠CBA
∵$\frac {EF}{AB}=\frac {FN}{AD}=\frac {MN}{CD}=\frac {EM}{BC}$
∴平行四边形ABCD∽平行四边形FEMN
∵点F、E、M、N分别是AO、BO、CO、DO的中点
∴EF 是△AOB的中位线,FN是△AOD的中位线,
MN是△COD的中位线,EM是△BOC的中位线
∴EF//AB,FN//AD,
$\frac {EF}{AB}=\frac {FN}{AD}=\frac {MN}{CD}=\frac {EM}{BC}=\frac {1}{2}$
∵EF//AB,FN//AD
∴∠EFO=∠BAO,∠NFO=∠DAO
∴∠EFN=∠BAD
同理可得:∠FNM=∠ADC,∠NME=∠DCB,∠MEF=∠CBA
∵$\frac {EF}{AB}=\frac {FN}{AD}=\frac {MN}{CD}=\frac {EM}{BC}$
∴平行四边形ABCD∽平行四边形FEMN
2. 如图,在平面直角坐标系中,△OAB 的顶点坐标分别为 O(0,0)、A(4,0)、B(0,2). 你能否在
x 轴、y 轴上分别找到格点 C、D,使得由点 O、C、D 组成的三角形与△AOB 相似(不含与
△AOB 全等)?如果能,请画出图形,并写出点 C、D 的坐标.

x 轴、y 轴上分别找到格点 C、D,使得由点 O、C、D 组成的三角形与△AOB 相似(不含与
△AOB 全等)?如果能,请画出图形,并写出点 C、D 的坐标.

答案:
解: C(2,0)、D(0,1)
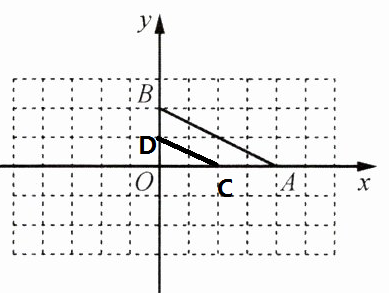
解: C(2,0)、D(0,1)
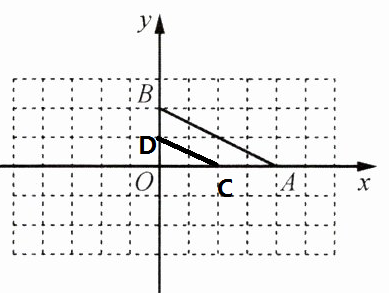
查看更多完整答案,请扫码查看


