《2026年伴你学九年级数学下册苏科版》

活动一:操作思考
1. 观察一副三角尺:(1)它们有几个不同的锐角？分别是多少度?(2)每块三角尺的三边之间有怎样的数量关系?试用不同的方法进行表述.
2. (1)请根据三角尺的三边关系确定$\sin 30^{\circ}、\cos 30^{\circ}、\tan 30^{\circ}$的值.
(2)你还能求出一副三角尺中其他锐角的三角函数值吗?

答案： 解：一副三角尺有三个不同的锐角，它们分别是​30°、​​45°、​​60°​
三边关系是​1：​​ 1：$​​\sqrt{2}​$或​1 ：$​​\sqrt{3}$：​​2​
解：$​sin 30°=\frac {1}{2}；$$​​cos 30°=\frac {\sqrt{3}}{2}；$$​​tan 30°=\frac {\sqrt{3}}{3}​$
解：$​sin 45°=cos 45°=\frac {\sqrt 2}{2}；$​​tan 45°=1​

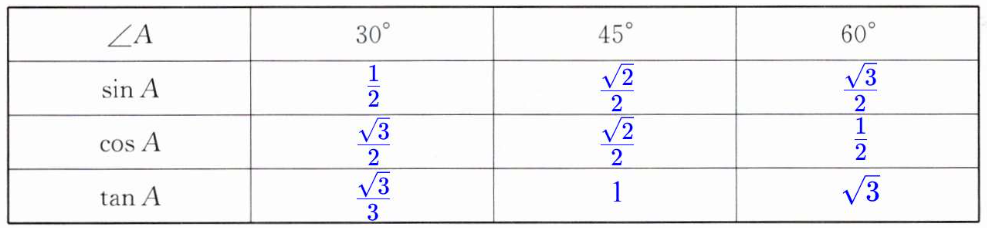
活动二:归纳结论

答案：

活动三:应用探索
利用特殊角的三角函数值,找出含特殊角的直角三角形的边角关系,并利用边角关系分别画出度数为$30^{\circ}、45^{\circ}、60^{\circ}$的角.

答案： 解：可以。
含​30°​的直角三角形的三边关系为​1 ：$\sqrt{3}$： 2​
可以画出​30°​和​60°​的角
​45°​的直角三角形的三边关系为​1 ： 1 ：$\sqrt{2}​$
可以画出​45°​的角

1. $\sin 60^{\circ}$的相反数是(C).

A.$-\frac{1}{2}$
B.$-\frac{\sqrt{3}}{3}$
C.$-\frac{\sqrt{3}}{2}$
D.$-\frac{\sqrt{2}}{2}$

答案： C

2. 已知$\alpha,\beta$是锐角,若$\sin\alpha=\frac{\sqrt{2}}{2},\cos\beta=\frac{\sqrt{2}}{2}$,则$\angle\alpha、\angle\beta$的大小关系是(C).

A.$\angle\alpha＞\angle\beta$
B.$\angle\alpha＜\angle\beta$
C.$\angle\alpha=\angle\beta$
D.$\angle\alpha = 2\angle\beta$

答案： C