第26页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
活动一:想一想,做一做
如图 5-9,河上有一座抛物线形拱桥,已知当桥下的水面离桥拱顶部 3 m 时,水面宽 AB 为 6 m,当水位上升 1 m 时,水面宽 CD 为多少米?


(1) 如图 5-10,以桥拱的最高点为原点,过原点的水平线为横轴,过原点的铅垂线为纵轴建立平面直角坐标系,把桥拱看作一个二次函数的图像,则相应的函数表达式为
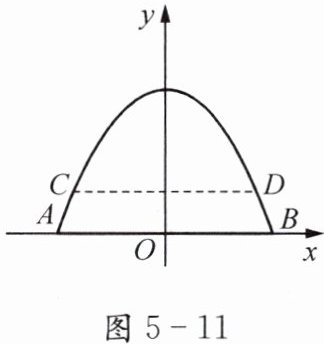
(2) 如图 5-11,以桥下水面宽 AB 的中点为原点,AB 所在的直线为横轴,过原点的铅垂线为纵轴建立平面直角坐标系,把桥拱看作一个二次函数的图像,则相应的函数表达式为
(3) 你还可以建立怎样的平面直角坐标系求 CD 的长度?
(4) 通过本问题的解决,你对解决与抛物线有关的实际问题有什么认识?
如图 5-9,河上有一座抛物线形拱桥,已知当桥下的水面离桥拱顶部 3 m 时,水面宽 AB 为 6 m,当水位上升 1 m 时,水面宽 CD 为多少米?



(1) 如图 5-10,以桥拱的最高点为原点,过原点的水平线为横轴,过原点的铅垂线为纵轴建立平面直角坐标系,把桥拱看作一个二次函数的图像,则相应的函数表达式为
$y=-\frac{1}{3}x^{2}$
,C、D 两点的坐标分别为$(-\sqrt{6},-2)、(\sqrt{6},-2)$
,CD 的长度为$2\sqrt{6}m$
.(2) 如图 5-11,以桥下水面宽 AB 的中点为原点,AB 所在的直线为横轴,过原点的铅垂线为纵轴建立平面直角坐标系,把桥拱看作一个二次函数的图像,则相应的函数表达式为
$y=-\frac{1}{3}x^{2}+3$
,C、D 两点的坐标分别为$(-\sqrt{6},1)、(\sqrt{6},1)$
,CD 的长度为$2\sqrt{6}m$
.(3) 你还可以建立怎样的平面直角坐标系求 CD 的长度?
(4) 通过本问题的解决,你对解决与抛物线有关的实际问题有什么认识?
答案:
$y=-\frac {1}{3}x^2 $
$(-\sqrt{6},$-2)、$(\sqrt{6},$-2)
$2\sqrt{6}m$
$y=-\frac {1}{3}x^2+3$
$(-\sqrt{6},$1)、$(\sqrt{6},$1)
$2\sqrt{6}m$
解:还可以以点A为原点,以AB所在直线为x轴,过原点的铅垂线为y轴建立平面直角坐标系。
解:先建立合适的平面直角坐标系,再确定二次函数,依据函数关系解决问题,是解决这类问题的一般思路。
$(-\sqrt{6},$-2)、$(\sqrt{6},$-2)
$2\sqrt{6}m$
$y=-\frac {1}{3}x^2+3$
$(-\sqrt{6},$1)、$(\sqrt{6},$1)
$2\sqrt{6}m$
解:还可以以点A为原点,以AB所在直线为x轴,过原点的铅垂线为y轴建立平面直角坐标系。
解:先建立合适的平面直角坐标系,再确定二次函数,依据函数关系解决问题,是解决这类问题的一般思路。
活动二:试一试,议一议
阅读思考课本的“拓展与延伸”,尝试写出解答思路.
阅读思考课本的“拓展与延伸”,尝试写出解答思路.
答案:
解:桥拱的函数表达式为$y= -\frac {1}{3}x²$
当x=2时,$y=-\frac {1}{3}×2²=-\frac {4}{3}>-2.5$
∴这艘船能从拱桥下通过。
当x=2时,$y=-\frac {1}{3}×2²=-\frac {4}{3}>-2.5$
∴这艘船能从拱桥下通过。
查看更多完整答案,请扫码查看


