第63页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
活动一:操作思考
1.(1)如图 7-1,一架梯子斜靠在墙上,当它的顶端向下滑动时,它的底端将如何运动?滑动前$(AB)$与滑动后$(A'B')$的梯子,哪一个更陡些?
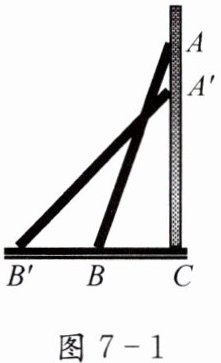
(2)在这一过程中变化的量有哪些?如何描述梯子在两个不同位置的倾斜程度呢?请具体分析研究.
2. 如图 7-2,如果两架梯子$AB$、$CD$靠在墙上,且$AB // CD$,这两架梯子的倾斜程度相同吗?描述这两架梯子倾斜程度的量有什么关系?试着说说理由.
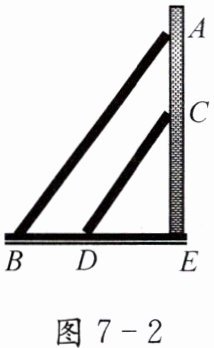
3. 思考课本中“观察与思考”中问题 2、3,你能获得什么结论?
4. 请你自学课本内容,了解在直角三角形中如何表示一个锐角的正切.
1.(1)如图 7-1,一架梯子斜靠在墙上,当它的顶端向下滑动时,它的底端将如何运动?滑动前$(AB)$与滑动后$(A'B')$的梯子,哪一个更陡些?

(2)在这一过程中变化的量有哪些?如何描述梯子在两个不同位置的倾斜程度呢?请具体分析研究.
2. 如图 7-2,如果两架梯子$AB$、$CD$靠在墙上,且$AB // CD$,这两架梯子的倾斜程度相同吗?描述这两架梯子倾斜程度的量有什么关系?试着说说理由.

3. 思考课本中“观察与思考”中问题 2、3,你能获得什么结论?
4. 请你自学课本内容,了解在直角三角形中如何表示一个锐角的正切.
答案:
解:梯子顶端向下滑动后,底端向左运动。
滑动前的梯子比滑动后的梯子更陡。
解:在这个过程中,梯子与水平面的夹角有变化梯子的顶端与点C之间的距离有变化,
梯子的底端与点C之间的距离也有变化;
梯子与水平线的夹角可以描述梯子的倾斜程度,梯子顶端与点C之间的距离,
梯子底端与点C之间的距离的比也可以描述梯子的倾斜程度。
解:直角三角形的一个锐角越大,其对边与邻边的比值越大;
一个锐角越小,其对边与邻边的比值越小。
解:当AB//CD时,这两架梯子的倾斜程度相同,
根据三角形相似,前面所提到的描述倾斜程度的量在这里分别对应相同。
滑动前的梯子比滑动后的梯子更陡。
解:在这个过程中,梯子与水平面的夹角有变化梯子的顶端与点C之间的距离有变化,
梯子的底端与点C之间的距离也有变化;
梯子与水平线的夹角可以描述梯子的倾斜程度,梯子顶端与点C之间的距离,
梯子底端与点C之间的距离的比也可以描述梯子的倾斜程度。
解:直角三角形的一个锐角越大,其对边与邻边的比值越大;
一个锐角越小,其对边与邻边的比值越小。
解:当AB//CD时,这两架梯子的倾斜程度相同,
根据三角形相似,前面所提到的描述倾斜程度的量在这里分别对应相同。
活动二:应用探究
1. 阅读课本例 1 并思考:
(1)求$\tan A$需要什么条件?缺少的条件如何解决?
(2)求$\tan B$.
2. 解决课本中的“思考与探索”.
1. 阅读课本例 1 并思考:
(1)求$\tan A$需要什么条件?缺少的条件如何解决?
(2)求$\tan B$.
2. 解决课本中的“思考与探索”.
答案:
解:
(1)需要已知BC和AC的长度。
缺少的BC的长度可以通过直角三角形的勾股定理来求。
解:$tan B=\frac {AC}{BC}=\frac {4}{3}$
(1)需要已知BC和AC的长度。
缺少的BC的长度可以通过直角三角形的勾股定理来求。
解:$tan B=\frac {AC}{BC}=\frac {4}{3}$
查看更多完整答案,请扫码查看


