《2026年伴你学九年级数学下册苏科版》

2. 求满足下列条件的锐角 $\alpha$(精确到 $0.01^{\circ}$).
(1)$\sin \alpha=\frac{1}{2}$；
(2)$\cos \alpha=0.2$；
(3)$\tan \alpha=3$.

答案： 解：​​
(1)​​
∵$​​sin 30° =\frac {1}{2}​​$
∴​​α=30°​​
​​​​
(2)​​
∵​​cos 78.46° ≈0.2​​
∴​​α=78.46°​​
(3)
∵​​tan 71.57°≈3​​
∴​​α=71.57°​​

3. 某商场要安装一部自动扶梯. 已知一、二楼之间层高为 3.4 m，可供电梯伸展的地面长度不超过 10 m. 求电梯的最小倾斜角(精确到 $0.01^{\circ}$).

答案： 解：
∵$​​tan α=\frac {3.4}{10}= 0.34 ​​$
由​​tan 18.75°≈0.34​​
∴最小倾斜角​​α=18.78°​​
答：电梯的最小倾斜角为​​18.78°。​​

1. 如图，一棵大树垂直于地面，小明测得 CB 的长度为 10 m，$\angle ACB = 50^{\circ}$，则树高 AB 约为12m(参考数据：$\sin 50^{\circ}\approx0.77$，$\cos 50^{\circ}\approx0.64$，$\tan 50^{\circ}\approx1.2$).

答案： 12

2. 已知三角函数值，用计算器求锐角 A 和 B，并总结规律：
(1)$\sin A = 0.3547$，$\cos B = 0.3547$；
(2)$\sin A = 0.65$，$\cos B = 0.65$；
(3)描述你发现的规律.

答案： 解：
(1) ∠A≈20.78°，∠B≈69.22°，由此可得∠A+∠B=90°
\
(2) ∠A≈40.54°，∠B≈49.46°
由此可得∠A+∠B=90°
\
(3)如果一个角的正弦值与另一个角的余弦值相等，那么这两个角互余

3. 你听说过意大利著名的比萨斜塔吗？为了研究物体的运动规律，有人曾经从 55 m 高的塔顶竖直丢下一个物体，它的着地点距塔底部 4.8 m，根据这两个数据估计斜塔偏离铅垂线的角度(精确到 $1'$).

答案： 解：
∵$​​tan α=\frac {4.8}{55}=0.087​​$
∴​​α≈4°59'​​
答：斜塔偏离铅垂线的角度是​​4°59'。​​

4. 已知三角函数值，可以先利用计算器求出锐角 $\alpha$ 与 $\beta$，从而比较它们的大小. 你能否不用计算器来比较以下的锐角 $\alpha$ 与 $\beta$ 的大小？如果能，说说你的想法.
(1)$\cos \alpha=\frac{3}{4}$，$\tan \beta=\frac{5}{4}$；
(2)$\sin \alpha=0.4$，$\cos \beta=0.51$.

答案：
解：​
(1)​构建一个直角三角形​ABC​

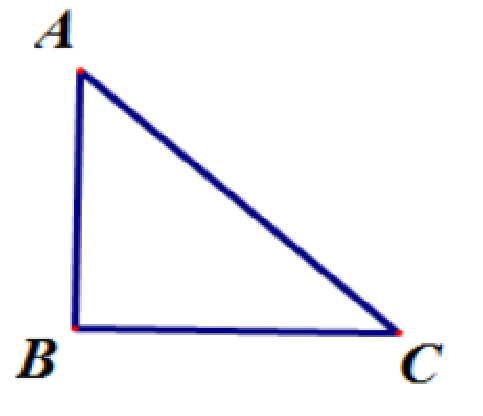
当​AB=3，​​AC=4​
∴$​cosA =\sqrt{AC²-AB²}=\sqrt{7}​$
$​tan α= tan A=\frac {BC}{AB}=\frac {\sqrt{7}}{3}​$
∵$​\sqrt{7}\lt 3​$
∴$​\frac {\sqrt{7}}{3}＜1＜\frac {5}{4}​$
∴$​tan α\lt tan β​$
∴$α\lt β$
​
(2)​构建直角三角形​ABC。​
当​BC=4，​​AC= 10​时
$​sinA=\frac {BC}{AC}= 0.4​$
$​AB=\sqrt{AC²-BC²}= 2\sqrt{21}​$
$​cos α= cos-A= \frac {AB}{BC}=\frac {\sqrt{21}}{5}≈0.92​$
∴​cosa＞cosβ​
∴$​a\lt β​$