《2025年全优标准卷七年级数学上册人教版》

22. (9 分)春节前夕,某商家预测某种水果能够畅销,就购进了第一批 200 斤这种水果,上市后销售非常好,商家又购进第二批这种水果,所购数量是第一批购进数量的 2 倍,但每斤的进价多了 5 元,已知第二批的进货总钱数比第一次多 8000 元.
(1) 该商家购进第一批这种水果时每斤多少元?
(2) 由于储存不当,第二批购进的水果中有 10% 腐坏,不能售卖. 该商家将两批水果按同一价格全部销售完毕后获利 8000 元,则每斤这种水果的售价是多少元?

答案： 22.解：
(1)设该商家购进第一批这种水果时每斤
x元，则该商家购进第二批这种水果时每斤
(x+5)元，
根据题意，得200x+8 000=2×200(x+5)，
解得x=30.
答：该商家购进第一批这种水果时每斤
30元.
(2)设每斤这种水果的售价是y元，
根据题意，得[200+2×200×(1-10%)]y-
200×30-2×200×(30+5)=8 000，
解得y=50.
答：每斤这种水果的售价是50元.

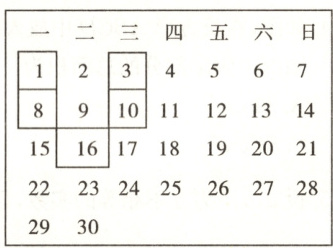
23. (9 分)如图所示的是 2024 年 4 月的日历表.
(1) 在图中用优美的“”U 形框框住五个数,其中最小的数为 1,求 U 形框中的五个数字之和;
(2) 在图中移动 U 形框的位置,框住的五个数字之和可以为 63 吗? 若能,求出这五个数字中最小的数;若不能,请说明理由.

答案： 23.解：
(1)由图可知，框住的5个数分别是1,8，
16,3,10，
$\because1+8+16+3+10=38，$
$\thereforeU$形框中的五个数字之和为38.
(2)框住的五个数字之和不可以为63，理由
如下：
设最小的数字为x，由
(2)可知这5个数的和
为5x+33，$\therefore5x+33=63，$解得x=6，
$\therefore$要求框出的5个数中最小的数是6，由图可
知，不能框出这样的5个数.

24. (12 分)如图,数轴上有 $ A,B,C $ 三个点,分别表示有理数 $ -10,-5,5 $,动点 $ P $ 从点 $ A $ 出发,以每秒 1 个单位的速度向终点 $ C $ 移动,移动时间为 $ t\ s $.
(1) 用含 $ t $ 的代数式表示点 $ P $ 对应的数字:-10+t;
(2) 当点 $ P $ 动到点 $ B $ 时,点 $ Q $ 从点 $ A $ 出发以每秒 3 个单位长度的速度向点 $ C $ 运动,点 $ Q $ 到达点 $ C $ 后,立即以同样的速度返回,运动到终点 $ A $ 时停止. 在点 $ Q $ 开始运动后:
① 用含 $ t $ 的代数式表示点 $ Q $ 的移动时间:(t-5)s;点 $ Q $ 未到达点 $ C $ 前,点 $ Q $ 到点 $ C $ 的距离 $ QC = $30-3t,点 $ Q $ 到达点 $ C $ 后,点 $ Q $ 到点 $ C $ 的距离 $ QC = $3t-30;
② $ P,Q $ 两点之间的距离能否为 3 个单位长度? 如果能,请求出此时 $ t $ 的值;如果不能,请说明理由.

答案： 24.解：
(1)-10+t
(2)①
∵动点P从点A 出发，到点B 所需的
时间为[-5-(-10)]÷1=5(s)，
$\therefore$点Q的移动时间为(t-5)s.
∵点Q未到达C前，
点Q表示的数为-10+3(t-5)=3t-25，
$\thereforeCQ=5-(3t-25)=30-3t;$
∵点Q从点A到点C所需的时间为[5-
(-10)]÷3=5(s)，
$\therefore$点Q到达点C后，
点Q表示的数为5-3(t-5-5)=35-3t，
$\thereforeCQ=5-(35-3t)=3t-30.$
故答案为：(t-5)s 30-3t 3t-30.
②P,Q两点之间的距离能为3个单位长度.
当点Q未到达点C前，点Q表示的数为3t-
25，点P表示的数为-10+t，
$\therefore$|3t-25-(-10+t)|=3，
解得t=6或t=9;
当点Q到达点C后，点Q表示的数为35-
3t，点P表示的数为-10+t，
$\therefore$|35-3t-(-10+t)|=3，
解得t=10.5或t=12.
综上所述，t的值为6或9或10.5或12.