《2025年全优标准卷七年级数学上册人教版》

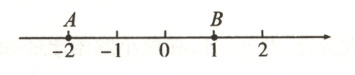
22. (8 分)如图,数轴上的 $A,B$ 两点表示的数分别为 $-2,1$. 把一张透明的胶片放置在数轴所在的平面上,并在胶片上描出线段 $A'B'$(点 $A,B$ 分别对应点 $A',B'$). 左右平移该胶片,平移后的点 $A'$ 表示的数为 $a$,点 $B'$ 表示的数为 $b$.

(1) 计算: $-2+1$;
(2) 若胶片向右平移 $m$ 个单位长度,求 $a+2b$ 的值. (用含 $m$ 的式子表示)

答案： 22.解：
(1)-2+1=-1.
(2)根据题意，得a+2b=(-2+m)+2(1+m)=3m.

23. (10 分)(1) 填空:$3^{1}-3^{0}=3^{($0$)}×2$;$3^{2}-3^{1}=3^{($1$)}×2$;$3^{3}-3^{2}=3^{($2$)}×2$;
(2) 探寻(1)中式子的规律,试写出第 $n$ 个等式,并说明第 $n$ 个等式成立;
(3) 计算:$3^{0}+3^{1}+3^{2}+·s+3^{2024}$.

答案： 23.解：$(1)3^{1}-3^{0}=3^{0}×2;3^{2}-3^{1}=3^{1}×2;3^{3}-3^{2}=3^{2}×2;$
故答案为：0 1 2.
(2)第n个等式是$3^{n}-3^{n-1}=3^{n-1}×2，$
理由如下：$3^{n}-3^{n-1}=3^{n-1}×(3-1)=3^{n-1}×2，$
故第n个等式是$3^{n}-3^{n-1}=3^{n-1}×2$成立.
(3)令$T=3^{0}+3^{1}+3^{2}+⋯+3^{2024}，$
则$3T=3^{1}+3^{2}+⋯+3^{2025}，$
∴$3T-T=3^{2025}-3^{0}，$
∴$T=\frac{3^{2025}-1}{2}，$
即$3^{0}+3^{1}+3^{2}+⋯+3^{2024}$的值是$\frac{3^{2025}-1}{2}.$

24. (10 分)对于数轴上任意一点 $P$,把与点 $P$ 相距 $a$ 个单位长度($a$ 是正数)的两点所表示的数分别记作 $x$ 和 $y$(其中 $x＜y$),并把 $x,y$ 这两个数叫作“点 $P$ 关于 $a$ 的对称数组”,记作 $M(P,a)=＜x,y＞$. 例如:原点 $O$ 表示数 0,原点 $O$ 关于 1 的对称数组 $M(O,1)=＜-1,1＞$.
(1) 如果点 $P$ 表示数 1,那么点 $P$ 关于 2 的对称数组是＜-1,3＞;
(2) 如果 $M(P,a)=＜2,4048＞$,那么点 $P$ 表示的数是2025, $a$ 的值是2023;
(3) 如果点 $P,Q$ 是数轴上的两个动点,$M(P,3)=＜x,y＞,M(Q,2)=＜m,n＞$,两点同时从原点出发反向运动,当 $|n - x|=3|y - m|$ 时,求点 $P,Q$ 之间的距离.

答案： 24.解：
(1)＜-1,3＞
(2)
∵M(P,a)=＜2,4048＞，
∴点P表示的数为(2+4048)÷2=2025，
a=2025-2=2023.
故答案为：2025 2023.
(3)
∵M(P,3)=＜x,y＞,M(Q,2)=＜m,n＞,
∴x=P-3,y=P+3,m=Q-2,n=Q+2.
∵|n-x|=3|y-m|,
∴|Q+2-P+3|=3|P+3-Q+2|，即|Q-P+5|=3|P-Q+5|.
①当Q-P+5=3(P-Q+5)时，Q-P+5=3(P-Q)+15，化简，得$Q-P=\frac{5}{2}；$
②当Q-P+5=-3(P-Q+5)时，化简，得Q-P=10.
综上所述，点P,Q之间的距离是$\frac{5}{2}$或10.