《2025年新课程学习指导南方出版社八年级数学上册华师大版》

4. 如图18,小丽同学制作某手工作品的第一、第二个步骤是：①先裁下一张长BC= 20cm,宽AB= 16cm的长方形纸片ABCD；②将纸片沿着直线AE折叠,点D恰好落在BC边上的点F处. 请你根据上述步骤解答下列问题：
(1)找出图中∠FEC的余角；
(2)计算EC的长.

答案：
(1)
∵ ∠EFC = 90° - ∠FEC（直角三角形两锐角互余），∠B = 90°
∴ ∠AFE = ∠D = 90°（折叠性质），∠BAF + ∠BFA = 90°，∠BFA + ∠EFC = 90°
∴ ∠BAF = ∠EFC
∵ ∠FEC + ∠EFC = 90°
∴ ∠FEC的余角为∠EFC和∠BAF
(2)
∵ Rt△ADE绕点A折叠得到Rt△AFE
∴ Rt△ADE ≌ Rt△AFE
∴ ∠AFE = 90°，AF = 16，EF = DE
设EC = x，则DE = EF = 16 - x
在Rt△ABF中由勾股定理得：AB² + BF² = AF² ，即16² + BF² = 20²
解得BF = 12
∴ FC = 20 - 12 = 8
在Rt△EFC中，EF² = EC² + FC² ，即(16 - x)² = x² + 8²
解得x = 6
即EC = 6

5. 如图19甲,分别以Rt△ABC三边为直径向外作三个半圆,其面积分别用$S_1、$$S_2、$$S_3$表示,则不难得出$S_1= S_2+S_3.$
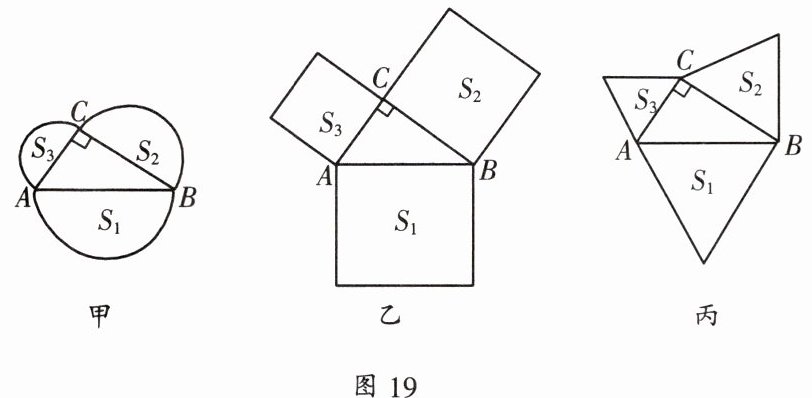
(1)如图19乙,分别以Rt△ABC三边为边向外作三个正方形,其面积分别用$S_1、$$S_2、$$S_3$表示,那么$S_1、$$S_2、$$S_3$之间有什么关系？
(2)如图19丙,分别以Rt△ABC三边为边向外作三个正三角形,其面积分别用$S_1、$$S_2、$$S_3$表示,请你确定$S_1、$$S_2、$$S_3$之间的关系,并加以说明.

答案：
(1)设Rt△ABC的三边BC、AC、AB的长分别为a、b、c，∠C=90°，则a²+b²=c²。
∵S₁=c²，S₂=a²，S₃=b²，
∴S₁=S₂+S₃。
(2)设Rt△ABC的三边BC、AC、AB的长分别为a、b、c，∠C=90°，则a²+b²=c²。
正三角形面积公式为S=√3/4×边长²，
∴S₁=√3/4c²，S₂=√3/4a²，S₃=√3/4b²，
∵a²+b²=c²，
∴√3/4a²+√3/4b²=√3/4c²，即S₂+S₃=S₁。
结论：S₁=S₂+S₃。