《2025年新课程学习指导南方出版社八年级数学上册华师大版》

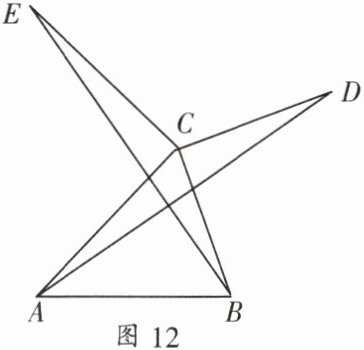
3. 如图12,过$\triangle ABC的顶点C作CE\perp AC$,$CD\perp CB$,且$CE = CA$,$CD = CB$. 求证：$AD = BE$.

答案： 证明：
∵ $CE \perp AC$，$CD \perp CB$，
∴ $\angle ACE = 90°$，$\angle BCD = 90°$。
∴ $\angle ACE + \angle ACB = \angle BCD + \angle ACB$，即 $\angle BCE = \angle DCA$。
在 $\triangle BCE$ 和 $\triangle DCA$ 中，
$\begin{cases} CB = CD \\\angle BCE = \angle DCA \\CE = CA \end{cases}$
∴ $\triangle BCE \cong \triangle DCA$（SAS）。
∴ $AD = BE$。

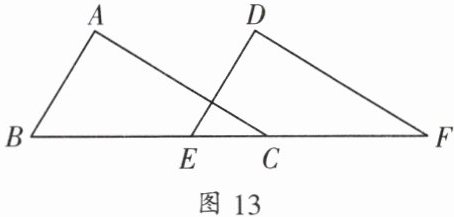
1. 如图 13,已知 $ AB \perp AC $,$ DE \perp DF $,$ AB // DE $,$ BE = CF $,则判定 $ \triangle ABC \cong \triangle DEF $ 的依据是AAS.

答案： AAS

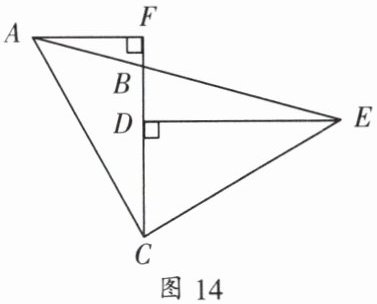
2. 如图 14,在 $ \triangle ACE $ 中,$ \angle ACE = 90° $,$ AC = CE $,$ ED \perp BC $ 于 $ D $,$ AF \perp CB $ 交 $ CB $ 的延长线于点 $ F $,则 $ AF $、$ DF $、$ CF $ 之间的数量关系是CF=AF+DF.

答案： CF=AF+DF

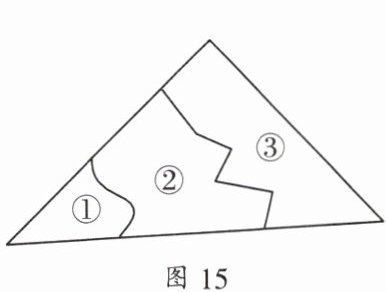
1. 小东同学不小心把一块三角形的修饰玻璃打破成了如图 15 所示的三块,现要到玻璃店去配一块完全一样的玻璃,那么最省事的方法是(C)

A.带①去
B.带②去
C.带③去
D.带①②去

答案： C

2. 在 $ \triangle ABC $ 和 $ \triangle A'B'C' $ 中,$ \angle A = \angle A' $,$ \angle B = \angle B' $,$ AB = A'B' $,则判定 $ \triangle ABC \cong \triangle A'B'C' $ 的方法是(B)
A.$ SAS $
B.$ ASA $
C.$ SSA $
D.$ AAS $

答案： B

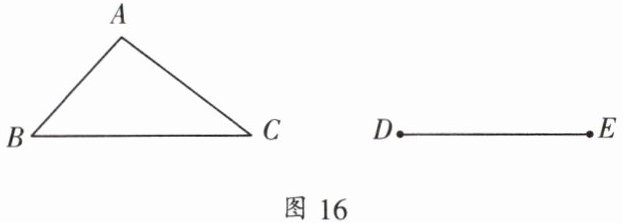
3. 如图 16,$ \triangle ABC $ 是不等边三角形,$ DE = BC $,以 $ D $、$ E $ 为两个顶点作位置不同的三角形,使所画的三角形与 $ \triangle ABC $ 全等,这样的三角形最多可以画出(C)

A.2 个
B.3 个
C.4 个
D.5 个

答案： C

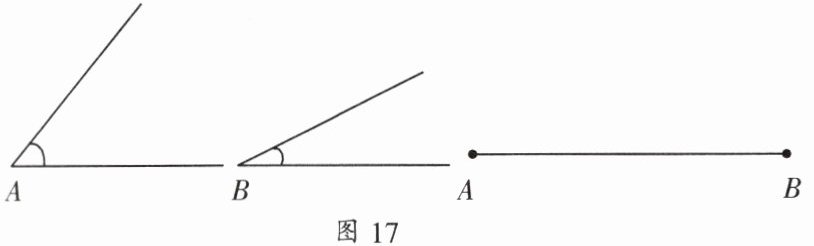
1. 如图 17,已知 $ \angle A $、$ \angle B $ 和线段 $ AB $,求作符合条件的 $ \triangle ABC $.

答案：
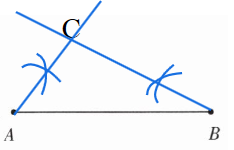
解：如图所示

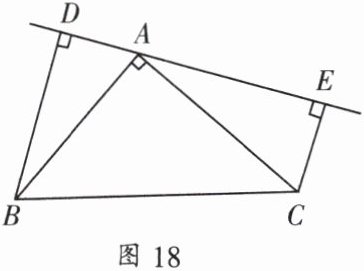
2. 如图 18,$ \angle BAC = 90° $,$ AB = AC $,$ BD \perp DE $,$ CE \perp DE $.试证明：$ DE = BD + CE $.

答案： 由题意知$BD \perp DE$，$CE \perp DE$，$\angle BAC = 90°$，
所以$\angle D = \angle E = 90°$，
因此$\angle DBA + \angle DAB = 90°$。
因为$\angle BAC = 90°$，
所以$\angle DAB + \angle EAC = 90°$，
等量代换可得$\angle DBA = \angle EAC$。
在$\triangle ABD$和$\triangle CAE$中，
$\begin{cases}\angle D = \angle E, \\\angle DBA = \angle EAC, \\AB = AC.\end{cases}$
所以$\triangle ABD \cong \triangle CAE (AAS)$。
因此$BD = AE$，$AD = CE$。
因为$DE = AD + AE$，
所以$DE = CE + BD$。