《2025年新课程学习指导南方出版社八年级数学上册华师大版》

2. 不用计算器,你能很快求出下列各式的结果吗？
(1) $\left(0.5× 3\frac{2}{3}\right)^{2024}\cdot \left(-2× \frac{3}{11}\right)^{2025}$
(2) $4^{2025}× 0.25^{2024}-8^{100}× \left(\frac{1}{2}\right)^{300}$

答案：
(1)
$\left(0.5×3\frac{2}{3}\right)^{2024}\cdot\left(-2×\frac{3}{11}\right)^{2025}$
$=\left(0.5×\frac{11}{3}\right)^{2024}\cdot\left(-2×\frac{3}{11}\right)^{2024}\cdot\left(-2×\frac{3}{11}\right)$
$=\left[0.5×\frac{11}{3}×(-2)×\frac{3}{11}\right]^{2024}\cdot\left(-\frac{6}{11}\right)$
$=(-1)^{2024}×\left(-\frac{6}{11}\right)$
$=1×\left(-\frac{6}{11}\right)$
$=-\frac{6}{11}$
(2)
$4^{2025}×0.25^{2024}-8^{100}×\left(\frac{1}{2}\right)^{300}$
$=4×4^{2024}×0.25^{2024}-2^{300}×\left(\frac{1}{2}\right)^{300}$
$=4×(4×0.25)^{2024}-(2×\frac{1}{2})^{300}$
$=4×1^{2024}-1^{300}$
$=4×1 - 1$
$=4 - 1$
$=3$

3. 用如图所示的几张卡片拼一些新的长方形,你有几种拼法？并计算它们的面积.

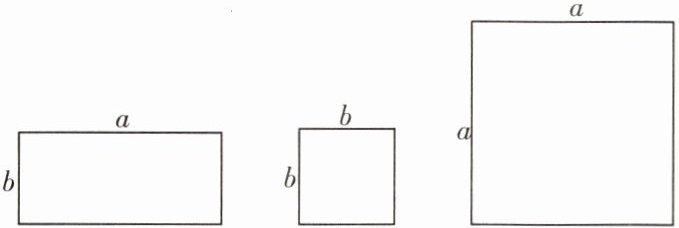
答案： 1. 首先分析拼法：
拼法一：将长为$a$宽为$b$的长方形与边长为$b$的正方形拼在一起。
此时新长方形的长为$(a + b)$，宽为$b$。
根据长方形面积公式$S=$长$×$宽，其面积$S_1=(a + b)× b$，根据乘法分配律$S_1=ab + b^{2}$。
拼法二：将长为$a$宽为$b$的长方形与边长为$a$的正方形拼在一起。
此时新长方形的长为$(a + b)$，宽为$a$。
根据长方形面积公式$S=$长$×$宽，其面积$S_2=(a + b)× a$，根据乘法分配律$S_2=a^{2}+ab$。
拼法三：将边长为$b$的正方形与边长为$a$的正方形拼在一起（$a\neq b$，若$a = b$，这种拼法与前面重复）。
此时新长方形的长为$(a + b)$，宽为$(a + b)$（特殊的长方形 - 正方形也是长方形的一种特殊情况），面积$S_3=(a + b)×(a + b)$，根据完全平方公式$S_3=a^{2}+2ab + b^{2}$。
拼法四：将长为$a$宽为$b$的长方形、边长为$b$的正方形、边长为$a$的正方形拼在一起。
此时新长方形的长为$(a + a + b)$（或$(a + b + b)$），宽为$b$（或$a$），若长为$(2a + b)$，宽为$b$，面积$S_4=(2a + b)× b=2ab + b^{2}$；若长为$(a + 2b)$，宽为$a$，面积$S_4=(a + 2b)× a=a^{2}+2ab$。
所以有$4$种拼法，面积分别为$ab + b^{2}$，$a^{2}+ab$，$a^{2}+2ab + b^{2}$，$a^{2}+2ab$（或$2ab + b^{2}$）。

4. 计算下列各式：
(1) $(x + 1)(x + 2)=$$x^{2}+3x + 2$；
(2) $(x + 3)(x - 2)=$$x^{2}+x - 6$；
(3) $(x - 1)(x - 3)=$$x^{2}-4x + 3$.
观察以上结果,你发现了什么规律？运用你发现的规律,直接说出$(x + 6)(x - 8)$的结果.
规律：对于$(x + a)(x + b)$，结果为$x^{2}+(a + b)x+ab$。$(x + 6)(x - 8)=x^{2}-2x - 48$

答案：
(1)
$(x + 1)(x + 2)$
$=x× x+x×2+1× x + 1×2$
$=x^{2}+2x+x + 2$
$=x^{2}+3x + 2$
(2)
$(x + 3)(x - 2)$
$=x× x+x×(-2)+3× x+3×(-2)$
$=x^{2}-2x+3x - 6$
$=x^{2}+x - 6$
(3)
$(x - 1)(x - 3)$
$=x× x+x×(-3)+(-1)× x+(-1)×(-3)$
$=x^{2}-3x - x + 3$
$=x^{2}-4x + 3$
规律：对于$(x + a)(x + b)$，结果为$x^{2}+(a + b)x+ab$。
对于$(x + 6)(x - 8)$，其中$a = 6$，$b=-8$，则$(x + 6)(x - 8)=x^{2}+(6 - 8)x+6×(-8)=x^{2}-2x-48$
答案依次为：
(1)$x^{2}+3x + 2$；
(2)$x^{2}+x - 6$；
(3)$x^{2}-4x + 3$；$(x + 6)(x - 8)=x^{2}-2x - 48$

[例 1]计算：$(-5x - 6y)(5x - 6y)$。

答案： 解：原式$=(-6y - 5x)(-6y + 5x)$
$=(-6y)^2 - (5x)^2$
$=36y^2 - 25x^2$