第60页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
1. $4$的平方根是(
A.$\pm 2$
B.$\sqrt{2}$
C.$2$
D.$16$
A
)A.$\pm 2$
B.$\sqrt{2}$
C.$2$
D.$16$
答案:
A
2. $64$的立方根等于(
A.$4$
B.$-4$
C.$8$
D.$-8$
A
)A.$4$
B.$-4$
C.$8$
D.$-8$
答案:
A
3. 如图1,数轴上点$P$所表示的数可能是(
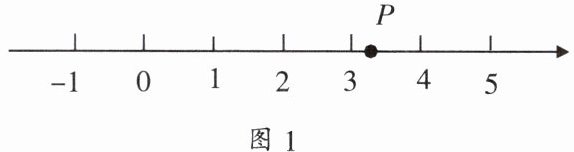
A.$\sqrt{6}$
B.$\sqrt{10}$
C.$\sqrt{17}$
D.$\sqrt{31}$
B
)
A.$\sqrt{6}$
B.$\sqrt{10}$
C.$\sqrt{17}$
D.$\sqrt{31}$
答案:
B
4. 下列运算正确的是(
A.$x^{5}-x^{3}= x^{2}$
B.$x^{4}(x^{3})^{2}= x^{10}$
C.$(-x^{12})÷ (-x^{3})= -x^{9}$
D.$(-2x)^{2}x^{-3}= 8$
B
)A.$x^{5}-x^{3}= x^{2}$
B.$x^{4}(x^{3})^{2}= x^{10}$
C.$(-x^{12})÷ (-x^{3})= -x^{9}$
D.$(-2x)^{2}x^{-3}= 8$
答案:
B
5. 计算$(-a)^{3}(-a)^{2}(-a^{5})$的结果是(
A.$a^{10}$
B.$-a^{10}$
C.$a^{30}$
D.$-a^{30}$
A
)A.$a^{10}$
B.$-a^{10}$
C.$a^{30}$
D.$-a^{30}$
答案:
A
6. 比较$2\sqrt{2}$,$3$,$\sqrt{7}$的大小,正确的是(
A.$\sqrt{7}<3<2\sqrt{2}$
B.$2\sqrt{2}<\sqrt{7}<3$
C.$2\sqrt{2}<3<\sqrt{7}$
D.$\sqrt{7}<2\sqrt{2}<3$
D
)A.$\sqrt{7}<3<2\sqrt{2}$
B.$2\sqrt{2}<\sqrt{7}<3$
C.$2\sqrt{2}<3<\sqrt{7}$
D.$\sqrt{7}<2\sqrt{2}<3$
答案:
D
7. 若$x^{2}-kx + 25$恰好是另一个整式的平方,则常数$k$的值为(
A.$4$
B.$10$
C.$-10$
D.$\pm 10$
D
)A.$4$
B.$10$
C.$-10$
D.$\pm 10$
答案:
D
8. 如图2,$AB// DE$,$AC// DF$,$AC = DF$,下列条件中,不能判断$\triangle ABC\cong\triangle DEF$的是(
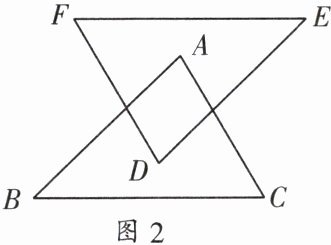
A.$AB = DE$
B.$\angle B= \angle E$
C.$EF = BC$
D.$EF// BC$
C
)
A.$AB = DE$
B.$\angle B= \angle E$
C.$EF = BC$
D.$EF// BC$
答案:
C
9. 有下列四种说法:
(1)负数没有立方根;
(2)$1的立方根与平方根都是1$;
(3)$\sqrt[3]{8}的平方根是\pm\sqrt{2}$;
(4)$\sqrt[3]{8+\frac{1}{8}}= 2+\frac{1}{2}= 2\frac{1}{2}$。
其中错误的说法有(
A.$1$个
B.$2$个
C.$3$个
D.$4$个
(1)负数没有立方根;
(2)$1的立方根与平方根都是1$;
(3)$\sqrt[3]{8}的平方根是\pm\sqrt{2}$;
(4)$\sqrt[3]{8+\frac{1}{8}}= 2+\frac{1}{2}= 2\frac{1}{2}$。
其中错误的说法有(
C
)A.$1$个
B.$2$个
C.$3$个
D.$4$个
答案:
C
10. 下列命题是真命题的是(
A.两个锐角之和一定是钝角
B.如果$x^{2}>0$,那么$x>0$
C.两直线平行,同旁内角相等
D.平行于同一条直线的两条直线平行
D
)A.两个锐角之和一定是钝角
B.如果$x^{2}>0$,那么$x>0$
C.两直线平行,同旁内角相等
D.平行于同一条直线的两条直线平行
答案:
D
11. 把多项式$a^{2}-2ab + b^{2}-1$分解因式,结果是(
A.$(a - b + 1)(a - b - 1)$
B.$(a - b + 1)(a + b - 1)$
C.$(a + b + 1)(a + b - 1)$
D.$(a + b + 1)(a - b - 1)$
A
)A.$(a - b + 1)(a - b - 1)$
B.$(a - b + 1)(a + b - 1)$
C.$(a + b + 1)(a + b - 1)$
D.$(a + b + 1)(a - b - 1)$
答案:
A
12. 如图3甲是一个边长为$m + n$的正方形,小颖将图甲中的阴影部分拼成图乙的形状,由图甲和图乙能验证的式子是(
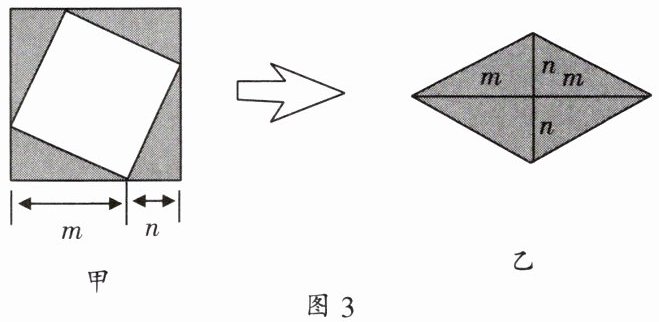
A.$(m + n)^{2}-(m - n)^{2}= 4mn$
B.$(m + n)^{2}-(m^{2}+n^{2})= 2mn$
C.$(m - n)^{2}+2mn= m^{2}+n^{2}$
D.$(m + n)(m - n)= m^{2}-n^{2}$
A
)
A.$(m + n)^{2}-(m - n)^{2}= 4mn$
B.$(m + n)^{2}-(m^{2}+n^{2})= 2mn$
C.$(m - n)^{2}+2mn= m^{2}+n^{2}$
D.$(m + n)(m - n)= m^{2}-n^{2}$
答案:
A
查看更多完整答案,请扫码查看


