《2025年新课程学习指导南方出版社八年级数学上册华师大版》

8. (综合题·代数与几何)如图 1,面积为$30\mathrm{cm}^2的正方形的四个角是面积为2\mathrm{cm}^2$的小正方形,现将四个角剪掉以后,制作成一个无盖的长方体,则这个长方体的底面边长和高分别是多少? (精确到$0.1\mathrm{cm}$)

答案： 设大正方形的边长为$a$ cm，小正方形的边长为$x$ cm，则长方体的底面边长为$a - 2x$ cm，高为$x$ cm。
根据题意，大正方形的面积为$a^2 = 30$，
小正方形的面积为$x^2 = 2$。
解得$a = \sqrt{30} \approx 5.477$（负值舍去），
$x = \sqrt{2} \approx 1.414$（负值舍去）。
所以长方体的底面边长为：
$a - 2x = \sqrt{30} - 2\sqrt{2} \approx 5.477 - 2 × 1.414 = 2.649 \approx 2.6$（$cm$），
高为：
$x = \sqrt{2} \approx 1.4$（$cm$）。
故这个长方体的底面边长约为$2.6cm$，高约为$1.4cm$。

9. (跨学科·数学计算)电视塔造得很高,是为了使从塔顶发射出来的电磁波像光的传播一样直线地射到较远的地方,而不被地球表面所挡住,从而使更大范围内的观众收看到电视节目. 已知传播半径$r(\mathrm{km})与电视塔的高度h(\mathrm{km})及地球的半径R(\mathrm{km})之间的关系式为r= \sqrt{2Rh}$,其中$R = 6370\mathrm{km}$. 现有一电视塔高为$196.2\mathrm{m}$,则电磁波的传播半径是多少? (精确到$1\mathrm{km}$)

答案： 已知$r = \sqrt{2Rh}$，$R = 6370\mathrm{km}$，$h = 196.2\mathrm{m} = 0.1962\mathrm{km}$。
$r=\sqrt{2×6370×0.1962}$
$=\sqrt{12740×0.1962}$
$\approx\sqrt{2499.588}$
$\approx50$
答：电磁波的传播半径约是$50\mathrm{km}$。

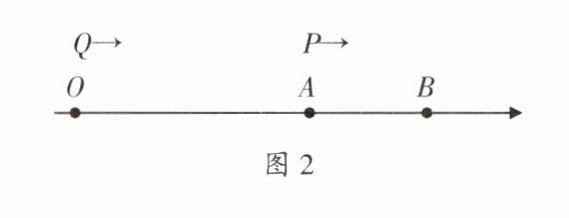
10. (综合题·动点模型)如图 2,数轴上$A、B两点对应的有理数分别为10和15$,点$P从点A$出发,以每秒$1$个单位长度的速度沿数轴正方向运动,点$Q同时从原点O$出发,以每秒$2$个单位长度的速度沿数轴正方向运动,设运动时间为$t$秒.
(1)当$0 ＜ t ＜ 5$时,用含$t$的式子填空:
$BP = $$5 - t$, $AQ = $$10 - 2t$;
(2)当$t = 2$时,求$PQ$的长;
(3)当$PQ = AB$时,求$t$的值.

(2)当$t=2$时，点$P$对应的数为$10+1×2=12$，点$Q$对应的数为$0+2×2=4$，所以$PQ=|12-4|=8$；
(3)因为$AB=15-10=5$，点$P$对应的数为$10+t$，点$Q$对应的数为$2t$，所以$PQ=|(10+t)-2t|=|10-t|$，当$PQ=AB$时，$|10-t|=5$，即$10-t=5$或$10-t=-5$，解得$t=5$或$t=15$。

答案：
(1)$5 - t$，$10 - 2t$；
(2)$8$；
(3)$t = 5$或$t = 15$。