《2025年新课程学习指导南方出版社八年级数学上册华师大版》

四、求下列方程中 $ x $ 的值
1. $ x^{2} = 49 $
2. $ 4x^{2} = 9 $

答案： 1.
$x^{2} = 49$
根据平方根的定义，
$x = \pm \sqrt{49}$
$x = \pm 7$
2.
$4x^{2} = 9$
方程两边同除以4，得
$x^{2} = \frac{9}{4}$
根据平方根的定义，
$x = \pm \sqrt{\frac{9}{4}}$
$x = \pm \frac{3}{2}$

五、已知 $ 2a - 1 $ 的平方根是 $ \pm 3 $,$ 3a + b - 1 $ 的平方根是 $ \pm 4 $,求 $ a + 2b $ 的平方根。

答案： $\pm 3$

1. $0.16$的算术平方根是$0.4$,$5$的算术平方根是$\sqrt{5}$。

答案： $0.4$；$\sqrt{5}$（对应填空依次填入）

2. $\sqrt{36}$ = 6；$\sqrt{(-3)^2}$ = 3；$-\sqrt{3^2}$ = -3；$\pm\sqrt{0.64}$ = ±0.8。

答案： 6；3； - 3；$\pm0.8$（按照题目顺序填写）

3. $\sqrt{16}$的算术平方根是2。

答案： $2$

4. $361$的算术平方根是19,平方根是$\pm19$。

答案： $19$；$\pm19$（第一个空填$19$，第二个空填$\pm19$）

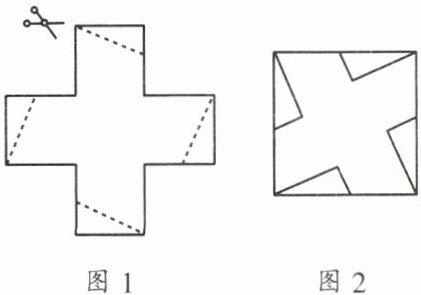
5. 将棱长为$1$的无盖正方体纸盒展开(如图1),沿虚线剪开,用得到的$5$张纸片(其中$4$张是完全相同的直角三角形纸片)拼成一个正方形(如图2)。则拼成的这个正方形边长为√5。

答案： √5

1. “$4的算术平方根是2$”表示为(D)
A.$\pm\sqrt{4}= \pm2$
B.$\sqrt{4}= \pm2$
C.$\pm\sqrt{4}= 2$
D.$\sqrt{4}= 2$

答案： D

2. 下列说法正确的是(C)

A.只有正数才有算术平方根
B.一个数的算术平方根一定是正数
C.一个非负数的算术平方根一定是非负数
D.$\sqrt{9}的算术平方根是3$

答案： C

3. 若式子$\sqrt{-a}$有意义,则(C)
A.$a＜0$
B.$a＞0$
C.$a\leq0$
D.$a\geq0$

答案： C

4. 若$\sqrt{x^2}= 3$,则$x$的值为(C)
A.$3$
B.$-3$
C.$\pm3$
D.无法确定

答案： C

5. 若$x$、$y$为有理数,且满足$\sqrt{2x - 1}+\sqrt{1 - 2x}+y = 4$,则$xy$的值为(C)
A.$0$
B.$\frac{1}{2}$
C.$2$
D.$-2$

答案： C

6. 面积为$2$的正方形的边长在(B)
A.$0和1$之间
B.$1和2$之间
C.$2和3$之间
D.$3和4$之间

答案： B

三、求下列各数的算术平方根
1. $1.21$
2. $\frac{4}{25}$
3. $4900$
4. $(-2)^4$

答案： 1.
$因为 1.1^2 = 1.21$，
所以$1.21$的算术平方根是$1.1$。
2.
$因为 (\frac{2}{5})^2 =\frac{4}{25}$，
所以$\frac{4}{25}$的算术平方根是$\frac{2}{5}$。
3.
$因为 70^2 = 4900$，
所以$4900$的算术平方根是$70$。
4.
$因为 (-2)^4 = 16$，且$4^2 = 16$，
所以$16$的算术平方根是$4$，
即$(-2)^4$的算术平方根是$4$。